Szia!

A lényeg röviden:
1. Ahhoz, hogy a kör egyenletét fel tudd írni egyedül a sugárra van szükséged, hiszen a középpont koordinátáit tudod.
2. A sugarat úgy tudod a legegyszerűbben kiszámolni, ha figyelembe veszed, hogy a sugár, tehát az O ponton áthaladó (vagy onnan induló teljesen mindegy) r egyenes merőleges lesz az érintőhöz húzott e egyenessel.
3. Mivel ezek merőlegesek ezért az ismeretlen r egyenesnek fel tudod írni az egyenletét (irányvektoros alakját), hiszen tudjuk, hogy ha két egyenes merőleges egymásra akkor az egyik egyenes egyik normálvektora egyenlő lesz a másik egyenes irányvektorával.
Miért jó ez nekünk, ha meghatározzuk a sugár egyenesének az egyenletét? Azért mert a kettő egymást metsző egyenes metszéspontja pontosan a köríven lesz, tehát ha kiszámoljuk a metszéspont koordinátáit amihez elengedhetetlen mind a két egyenes egyenlete, akkor meg tudjuk határozni az M metszéspont, és O középpont közötti távolságot. És ugye MO=r
4. Az érintő e egyenes normálvektora n(2;1), tehát az r egyenes irányvektora v(2;1). Ezt behelyettesítve az irányvektoros alakba (a -3;-2 ponttal, hiszen ezen átmegy az r egyenes) kapjuk, hogy r egyenes egyenlete: x-2y=1
5. Ha a két egyenletből álló egyenletrendszert megoldjuk, akkor megkapjuk a metszéspont koordinátáit, ezek: M(1,4;0,2)
6. Kiszámoljuk az MO szakaszt az ismert képlettel, erre kapjuk, hogy: 4,91, tehát ekkora a körnek a sugara.
7. Így a kör egyenlete: (x+3)^2+(y+2)^2=24,11
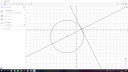
Az csatolt képen látható a kapcsolódó GeoGebras rajz.
Remélem, hogy tudtam segíteni, ha van valami kérdésed akkor írj nyugodtan!