Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Segitséget szeretnék
 nagyad1
kérdése
nagyad1
kérdése
840
Határozza meg a x^2+y^2=25 egyenletű kör és az y=15-x egyenletű egyenes metszéspontjainak koordinátáit.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
A metszéspont koordinátái kielégítik mindkét alakzat egyenletét. Vagyis a megadott egyenleteket mint egyenletrendszert kell megoldanunk:
`x^2+y^2=25`
`y=15-x`
Helyettesítsük be a kör egyenletébe az egyenes egyenletét:
`x^2+(15-x)^2=25`
Ezzel az egyik változót kiküszöböltük. Bontsuk fel a zárójelet:
`x^2+225-30x+x^2=25`
`2x^2-30x+200=0`
`x^2-15x+100=0`
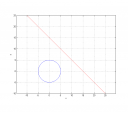
Egy másodfokú egyenletet kaptunk `x`-re. Viszont a diszkrimináns negatív (`15^2-400=-175`), vagyis az egyenletrendszernek nincs valós megoldása, a megadott alakzatok nem metszik egymást. Ezt egyébként számolás nélkül is könnyű látni, ha felvázolod az alakzatokat: egy origó középpontú, 5 egység sugarú kört, valamint egy egyenest, amely mindkét tengelyt a 15-nél metszi.
`x^2+y^2=25`
`y=15-x`
Helyettesítsük be a kör egyenletébe az egyenes egyenletét:
`x^2+(15-x)^2=25`
Ezzel az egyik változót kiküszöböltük. Bontsuk fel a zárójelet:
`x^2+225-30x+x^2=25`
`2x^2-30x+200=0`
`x^2-15x+100=0`
Egy másodfokú egyenletet kaptunk `x`-re. Viszont a diszkrimináns negatív (`15^2-400=-175`), vagyis az egyenletrendszernek nincs valós megoldása, a megadott alakzatok nem metszik egymást. Ezt egyébként számolás nélkül is könnyű látni, ha felvázolod az alakzatokat: egy origó középpontú, 5 egység sugarú kört, valamint egy egyenest, amely mindkét tengelyt a 15-nél metszi.
Módosítva: 6 éve
0
- Még nem érkezett komment!