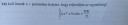Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Improprius integrál
 Attila089
kérdése
Attila089
kérdése
551
Valaki kerem levezetne nekem?
Jelenleg 1 felhasználó nézi ezt a kérdést.
analízis, integrál, paraméter
analízis, integrál, paraméter
0
Középiskola / Matematika
Válaszok
1 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
Ez nem improprius integrál, hanem sima Riemann.
A `c` paraméter az integrálás szempontjából konstans, tehát az integrálás linearitását kihasználva így írható a kifejezés:
`I=int_c^(2c) (cx^2+5c) dx``=``c* int_c^(2c) x^2 dx+5c * int_c^(2c) dx`
`x^2` primitívfüggvénye `x^3/3`, az egységé pedig `x`:
`I=c*[x^3/3]_c^(2c)+5c*[x]_c^(2c)``=``c((8c^3)/3-c^3/3)+5c(2c-c)``=``7/3c^4+5c^2`
Azt szeretnénk, hogy ez `100/21` legyen:
`7/3c^4+5c^2=100/21`
Vezessük be a `d=c^2` segédváltozót! Ezzel sima másodfokú egyenletet kapunk:
`7/3d^2+5d-100/21=0`
`49d^2+105d-100=0`
`d_{1,2}=(-105 pm sqrt(30625))/98=(-105 pm 175)/98`
Innen `d_1=5/7` és `d_2=-20/7`. Ezekből még vissza kell számolnunk a `c`-ket a `d=c^2` egyenlet alapján. Mindkét `d`-hez van két-két `c`, a megoldások tehát:
`c_1=sqrt(5/7)`
`c_2=-sqrt(5/7)`
`c_3=i*sqrt(20/7)=i*2sqrt(5/7)`
`c_4=-i*sqrt(20/7)=-i*2sqrt(5/7)`
Ellenőrzés: https://bit.ly/2WHq3kX
Ha komplex számokról még nem tanultál, akkor az utóbbi két megoldást figyelmen kívül hagyhatod, és azt mondhatod, hogy a negatív `d`-hez nem tartozik valós `c`.
A `c` paraméter az integrálás szempontjából konstans, tehát az integrálás linearitását kihasználva így írható a kifejezés:
`I=int_c^(2c) (cx^2+5c) dx``=``c* int_c^(2c) x^2 dx+5c * int_c^(2c) dx`
`x^2` primitívfüggvénye `x^3/3`, az egységé pedig `x`:
`I=c*[x^3/3]_c^(2c)+5c*[x]_c^(2c)``=``c((8c^3)/3-c^3/3)+5c(2c-c)``=``7/3c^4+5c^2`
Azt szeretnénk, hogy ez `100/21` legyen:
`7/3c^4+5c^2=100/21`
Vezessük be a `d=c^2` segédváltozót! Ezzel sima másodfokú egyenletet kapunk:
`7/3d^2+5d-100/21=0`
`49d^2+105d-100=0`
`d_{1,2}=(-105 pm sqrt(30625))/98=(-105 pm 175)/98`
Innen `d_1=5/7` és `d_2=-20/7`. Ezekből még vissza kell számolnunk a `c`-ket a `d=c^2` egyenlet alapján. Mindkét `d`-hez van két-két `c`, a megoldások tehát:
`c_1=sqrt(5/7)`
`c_2=-sqrt(5/7)`
`c_3=i*sqrt(20/7)=i*2sqrt(5/7)`
`c_4=-i*sqrt(20/7)=-i*2sqrt(5/7)`
Ellenőrzés: https://bit.ly/2WHq3kX
Ha komplex számokról még nem tanultál, akkor az utóbbi két megoldást figyelmen kívül hagyhatod, és azt mondhatod, hogy a negatív `d`-hez nem tartozik valós `c`.
Módosítva: 6 éve
0
- Még nem érkezett komment!