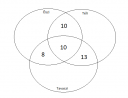
a) A képen látható a kitöltés. Itt az a lényeg, hogy amikor azt mondják, hogy '20-an voltak, akik az őszi és téli koncerten is szerepeltek", akkor abban azok is benne vannak, akik mindhármon ott voltak, tehát akik az őszin és télin voltak, de a tavaszin nem, 20-10=10, a többi ugyanígy.

b) Akik csak 1 helyen szerepeltek, azok mint az ábra üres részén találhatóak, tehát akiket beírtunk, azokat ki kell vonni a létszámból: 188-10-10-8-13=147 tanuló. Jelöljük azok számát T-vel, akik csak a tavaszin voltak, ekkor a szöveg szerint a télin T/2 tanuló vett részt, az őszin T/4-en voltak, ha ezeket összeadjuk, 147-et kell kapnunk:

T + T/2 + T/4 = 147 | *4
4T+2T+T=588
7T=588, erre T=84 adódik, tehát 84-en voltak tavasszal, 84/2=42-en télen és 84/4=21-en ősszel.

c) Összes eset: 60 gyerekből csinálunk 10 fős csoportot úgy, hogy sorrendjük nem számít: (60 alatt a 10)
Kedvező esetek száma: mivel nem számít a sorrendjük, ezért 1 konkrét esettel számolhatunk, legyen ez AAAAABBBBB, ekkor az a kérdés, hogy az 5 A helyre hányféleképpen választhatóak diákok: 32*31*30*29*28, de mivel ezen belül a sorrendjük nem számít, ezért osztunk 5!-sal: 32*31*30*29*28/5!=201376. A BBBBB részre ugyanez a helyzet: 28*27*26*25*24/5!=98280, így összesen 201376*98280=19791233280-féleképpen lehet bepakolni a gyerekeket.
Valószínűség: 19791233280/(60 alatt a 10)=~0,265=26,5%.