És mi a gondod?
Teljes négyzetté alakítva: (2/3 * (x - 9/10)^(2)) - 79/100

Ez akar lenni a feladat:

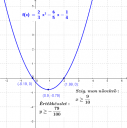
x→(2/3)*x²-(6/5)x-(1/4) ?

Az ilyen feladatokat általában úgy kezdjük, hogy teljes négyzetté alakítunk, ám ebben az esetben igencsak macerás lenne ennek felírása. A teljes négyzetes alakból többek a szélsőérték helye és értéke is kiolvasható, de szerencsére a szélsőérték helye máshogyan is meghatározható; tudjuk, hogy a függvény képe egy parabola, ami egy szimmetrikus alakzat, ami azt jelenti, hogy a gyökök (vagyis ahol a függvényérték 0) is szimmetrikusan helyezkednek el, tehát meg kell oldanunk a

0=(2/3)*x²-(6/5)x-(1/4) egyenletet, de szerencsére ennek kiszámolását is meg tudjuk úszni; a függvénytranszformációk szerint, ha egy függvényhez hozzáadunk egy konstanst (számot), akkor az y-tengellyel párhuzamosan mozog a képe, tehát a szélsőérték helye nem fog változni. Adjunk hozzá a függvényhez 1/4-et, ekkor egy sokkal barátságosabb egyenletet kapunk:

0=(2/3)*x²-(6/5)x, ebből ki tudunk emelni x-et:
0=x*((2/3)x-6/5)), ez akkor lesz 0, ha vagy x=0, vagy (2/3)x-(6/5)=0, tehát x=18/10=9/5. Most azt a számot keressük, amelyik a 0-tól és a 9/5-től egyenlő távolságra van, ez a (9/5)/2=9/10, és ha ezt beírjuk az eredetibe, meg is tudjuk, mennyi lesz az értéke:

(2/3)*(9/10)²-(6/5)*(9/10)-(1/4)=(2/3)*(81/100)-(6/5)*(9/10)-(1/4)=

=(162/300)-(54/50)-(1/4)=(27/50)-(27/25)-(1/4), ha megnézzük, ezek tizedestörtértéke mind véges, tehát most egyszerűbb úgy számolni, hogy átírjuk: 0,54-1,08-0,25=-0,79, tehát az eredeti függvény teljes négyzetes alakja:

(2/3)*(x-(9/10))²-0,79, 9/10 is átírható:

(2/3)*(x-0,9)²-0,79

Ebből már minden leolvasható; mivel a négyzetes tag értéke vagy 0 vagy pozitív, ezért a függvény értéke legalább -0,79, tehát a függvény értékkészlete: y≥-0,79.

Mononitás: nagy valószínűséggel láttál már parabolát, így nem nehéz rájönni, hogy ha x>0,9, akkor a függvény szigorúan monoton nő, ha x<0,9, akkor szigorúan monoton csökken, x=0,9 esetén szélsőértéke van.

Ha valami nem világos, várom kérdéseidet.