Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Koordináta geometria
 vanicsekkristof
kérdése
vanicsekkristof
kérdése
1241
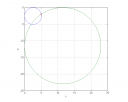
Egy kör érinti a két koordinátatengelyt,és átmegy az (5 ; -2) ponton.Írja fel az egyenletét!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 AlBundy
{ Polihisztor }
válasza
AlBundy
{ Polihisztor }
válasza
Ha érinti mindkét koordinátatengelyt, akkor a középpontja rajta van az `y=x` vagy az `y=-x` egyenesen. Mivel a megadott pont a IV. síknegyedben van, az `y=-x` egyenest választjuk. Tehát a középpont `(c; -c)` alakú. Továbbá azt is tudjuk, hogy az ilyen kör sugara `c`. A kör egyenlete:
`(x-c)^2+(y+c)^2=c^2`
Mivel a kör átmegy a megadott ponton, az egyenletet ki kell elégítenie, ebből van egy másodfokú egyenletünk `c`-re:
`(5-c)^2+(-2+c)^2=c^2`
`25+c^2-10c+4+c^2-4c=c^2`
`c^2-14c+29=0`
Ennek két valós megoldása van: `c_{1,2}=7 pm 2sqrt(5)`. Tehát két ilyen kör van:
`(x-7-2sqrt(5))^2+(y+7+2sqrt(5))^2=(7+2sqrt(5))^2`
`(x-7+2sqrt(5))^2+(y+7-2sqrt(5))^2=(7-2sqrt(5))^2`
`(x-c)^2+(y+c)^2=c^2`
Mivel a kör átmegy a megadott ponton, az egyenletet ki kell elégítenie, ebből van egy másodfokú egyenletünk `c`-re:
`(5-c)^2+(-2+c)^2=c^2`
`25+c^2-10c+4+c^2-4c=c^2`
`c^2-14c+29=0`
Ennek két valós megoldása van: `c_{1,2}=7 pm 2sqrt(5)`. Tehát két ilyen kör van:
`(x-7-2sqrt(5))^2+(y+7+2sqrt(5))^2=(7+2sqrt(5))^2`
`(x-7+2sqrt(5))^2+(y+7-2sqrt(5))^2=(7-2sqrt(5))^2`
0
- Még nem érkezett komment!