Mondjuk `h` magasan repül, és a földön `d` távolságra van kezdetben a vár (tehát nem egyenes vonalban van `d` távolságra, hanem ha pont a repülő alatt lenne az árnyéka, akkor az árnyék és a vár távolsága `d`).
Rajzold ezt fel. Kösd össze a várat a repülővel, lesz egy derékszögű háromszög, amiben felírható ez a szögfüggvény:
`h/d="tg"\ 35°=...` nézd meg a számológépeden.

Aztán rajzold fel felülnézetből is, csak a `d` lesz rajta, a `h` nem. Egy perc vagyis `1/60` óra múlva a repülő kelet felé lesz `600"km"/"h"·1/60"h"=10\ "km"`-re. Rajzold be ezt a 10 km-t is a rajzba (nem tudod élethűen rajzolni, mert `d` nem ismert, szóval csak úgy akárhogy). Végül kösd össze a gép végső pozícióját (mármint az árnyékának a pozícióját) a várral. Most is egy derékszögű háromszöget rajzoltál, ki tudod számolni a gép árnyékának és a várnak az új távolságát Pitagorasszal. Nevezük `d_2`=nek:
`d_2^2=d^2+10^2`

Aztán rajzold fel az új helyen is a repülőt magasan, alul a várral. Most is `h` magasan van a repülő, árnyékának a távolsága a vártól `d_2`. Kösd össze a repülőt a várral, háromszög lesz, ahol a tangens:
`h/d_2="tg"\ 25°=...` nézd meg a számológépeden.

Mondjuk az első egyenletből fejezd ki `d`-t (benne marad a `h` is), aztán a második egyenletbe azt írd bele, ezzel kifejezted `d_2^2`-t (abban `h^2` lesz). A `d_2^2`-t írd be a harmadik egyenlet négyzetébe és számold ki belőle `h^2`-t, aztán `h`-t.

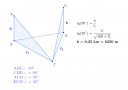
Úgy látom d-vel és d_2 -vel van jelölve, amit l_1, l_2 -vel jelöltem:

Legyen
α = 35° - az első pontban
β = 25°- a második pontban mért depresszió szög
S - a két mérés közt megtett távolság
H = ? - a keresett magasság

A feladat zárt megoldása
(H/tgβ)² - (H/tgα)²=S²
Ebből
H=S*tgα*tgβ/√ tg²α-tg²β 

vagy
(H*ctgβ)² - (H*ctgβ)² = S²
amiből
H = S/√ ctg²β - ctg²α 

Ha valaki nem kedvelné "tangenséket" azoknak
H=S*sinα*sinβ/√ sin(α-β)*sin(α+β)