Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Allapot-ter egyenletek szimulacio (scilab)
 MathOverflow
kérdése
MathOverflow
kérdése
747
Sziasztok!
Megoldottam a mellekelt atviteli fuggvenyeket. Most ezeket az allapot-ter egyenleteket kellene lemodellezni scilab nevezetu programban (matlab-hoz hasonlo).
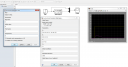
A megfelelő paramétereket kell bevinni az Xcos szimulációba.Ehhez a State Space dobozt kell használni az Xcosban.
Azonban nem tudom milyen parameterek...hogyan is aljak neki.. Aki jartas a temaban es segitene annak nagyon megkoszonnem !!
(Egyebkent nem egy bonyolult szimulacio,sot...,csak nem tudom miket kellene parameterkent beirogatnom,meg miket miert huzzak be xcosba..) Aki ert hozza, annak egyszeru
Megoldottam a mellekelt atviteli fuggvenyeket. Most ezeket az allapot-ter egyenleteket kellene lemodellezni scilab nevezetu programban (matlab-hoz hasonlo).
A megfelelő paramétereket kell bevinni az Xcos szimulációba.Ehhez a State Space dobozt kell használni az Xcosban.
Azonban nem tudom milyen parameterek...hogyan is aljak neki.. Aki jartas a temaban es segitene annak nagyon megkoszonnem !!
(Egyebkent nem egy bonyolult szimulacio,sot...,csak nem tudom miket kellene parameterkent beirogatnom,meg miket miert huzzak be xcosba..) Aki ert hozza, annak egyszeru

Jelenleg 1 felhasználó nézi ezt a kérdést.
scilab, allapot, tér, egyenletek
scilab, allapot, tér, egyenletek
0
Felsőoktatás / Matematika
Válaszok
6 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
Ahhoz, hogy leszimuláld a megadott rendszert, nem is kellett volna semmit sem számolni, mert az átviteli függvényt közvetlenül is be lehet vinni, erre való a "Continuous transfer function" doboz. Persze ha külön kérte a feladat, hogy állapotteres alakban kell bevinni, az más. Helyesen kiszámoltad az állapotteres leírás mátrixait, csak ezeket kell bepötyögni egy "Continuous state-space system" dobozba:
`A=[[0,1,0],[0,0,1],[-24,-26,-9]]`
`B=[[0],[0],[1]]`
`C=[[2,7,1]]`
`D=0`
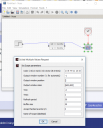
Aztán hogy mit akarsz szimulálni, azt neked kell tudnod. Gondolom, kell valami bemenetet adni a rendszernek, és ábrázolni kell a kimenetet. Scilabom nincs, de egy nagyon hasonló MATLAB Simulink megoldást mellékeltem, én itt egy egységugrást adtam a bemenetre, tehát a kimeneten a rendszer ugrásválaszát látjuk.
`A=[[0,1,0],[0,0,1],[-24,-26,-9]]`
`B=[[0],[0],[1]]`
`C=[[2,7,1]]`
`D=0`
Aztán hogy mit akarsz szimulálni, azt neked kell tudnod. Gondolom, kell valami bemenetet adni a rendszernek, és ábrázolni kell a kimenetet. Scilabom nincs, de egy nagyon hasonló MATLAB Simulink megoldást mellékeltem, én itt egy egységugrást adtam a bemenetre, tehát a kimeneten a rendszer ugrásválaszát látjuk.
1
-
MathOverflow: Nagyon szepen koszonom eloszor is a segitseget! 6 éve 0
-
MathOverflow: A feladat igazabol: 1.Kérem az átviteli függvény átalakításának levezetését ----- ezt en megcsinaltam, amit kepent mellektem. 6 éve 0
-
MathOverflow: 2.Miután megkapták az állapot-tér egyenleteket, a megfelelő paramétereket kell bevinni az Xcos szimulációba, ahogy órán is csináltuk. Ehhez a State Space dobozt kell használni az Xcosban. 6 éve 0
-
MathOverflow: (Készítsenek a szimuláció minden részletéről képernyőképet és azt is dokumentálják a doksiban.) 6 éve 0
-
MathOverflow: Hogy mit kell leszemulalni nem igazan tudom, de szerintem is csak valamilyen bementetet kell adni a rendszernek. 6 éve 0
 MathOverflow
válasza
MathOverflow
válasza
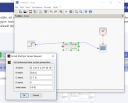
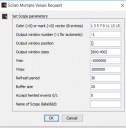
Ahogy nalad is, beirtam en is a parametereket. Viszont az initial state reszhez nem tudom mit kellene irnom. Ha pl. 0 0 5-t adok meg, lesz egy kis gorbe benne az elejen. (Illetve a CLOCK periodot atirtam 0.0001-re, igy latni valamennyire a valtozast)
(Es meg atirtam a Ymin(=-2) Ymax(=2) erteket, ahogy jol neztem nalad is, hogy jobban lathato legyen a valtozas.)
Ez igy viszonlag jo? Initial state-t nem tudom mit jelent, mit kellene oda irnom.
Nagyon-nagyon koszonom szepen a segitseged!
Eletmento tenyleg!
(Es meg atirtam a Ymin(=-2) Ymax(=2) erteket, ahogy jol neztem nalad is, hogy jobban lathato legyen a valtozas.)
Ez igy viszonlag jo? Initial state-t nem tudom mit jelent, mit kellene oda irnom.
Nagyon-nagyon koszonom szepen a segitseged!
Eletmento tenyleg!
0
- Még nem érkezett komment!
 AlBundy
{ Polihisztor }
válasza
AlBundy
{ Polihisztor }
válasza
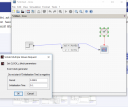
Az initial state azt jelenti, hogy kezdeti állapot. Vagyis az állapotváltozóidnak (`x_1`, `x_2`, `x_3`) a `t=0` időpontbeli értéke (egy kicsit pontosabban: a nullabeli bal oldali határértéke). Ha nem adtak meg semmi egyebet, akkor ez legyen nullvektor, tehát induljon energiamentes állapotból a rendszer. Ez a funkció például olyankor nagyon hasznos, ha az állapotváltozós leírásod egy rugós rendszert modellez, és arra vagy kíváncsi, hogy hogyan viselkedik a rendszer, ha az összenyomott rugót elengeded, és magára hagyod. Vagy ha egy feltöltött kondenzátorra egyszer csak rákapcsolsz egy tekercset, és még lehetne sorolni a példákat.
A clock perioddal kapcsolatban megnéztem a Scilab online dokumentációját. Az az óra csak annyit csinál, hogy a beállított gyakorisággal generál eseményeket, a scope pedig ekkor mintavételezi a jelet és kirajzolja az értéket.
A képeid ígéretesek, az ugrásválasz úgy néz ki, mint nálam, de én egy kicsit jobban "belezoomolnék" a jelbe a scope Ymin és Ymax paraméterének összébb húzásával, hogy jól leolvasható legyen a végérték.
Apropó végérték... Ezzel valamennyire ellenőrizni is tudod a szimuláció helyességét, mert az ugrásválasz végértékét könnyen ki tudjuk számolni. Ugyanis a Laplace-transzformáció végértéktétele szerint az ugrásválasz állandósult állapotbeli értéke:
`lim_(p->0)(p^2+7p+2)/(p^3+9p^2+26p+24)``=``(0+7*0+2)/(0+9*0+26*0+24)``=``1/12~~0.0833`
A clock perioddal kapcsolatban megnéztem a Scilab online dokumentációját. Az az óra csak annyit csinál, hogy a beállított gyakorisággal generál eseményeket, a scope pedig ekkor mintavételezi a jelet és kirajzolja az értéket.
A képeid ígéretesek, az ugrásválasz úgy néz ki, mint nálam, de én egy kicsit jobban "belezoomolnék" a jelbe a scope Ymin és Ymax paraméterének összébb húzásával, hogy jól leolvasható legyen a végérték.
Apropó végérték... Ezzel valamennyire ellenőrizni is tudod a szimuláció helyességét, mert az ugrásválasz végértékét könnyen ki tudjuk számolni. Ugyanis a Laplace-transzformáció végértéktétele szerint az ugrásválasz állandósult állapotbeli értéke:
`lim_(p->0)(p^2+7p+2)/(p^3+9p^2+26p+24)``=``(0+7*0+2)/(0+9*0+26*0+24)``=``1/12~~0.0833`
1
-
MathOverflow: Nagyon szépen köszönöm! Még lenne egy tényleg utolsó kérdésem, válaszként mellékelem a képet hozzá. Megcsináltam ezek alapján egy hasonló feladatot, azonban kicsit más az ábra amit kaptam. 6 éve 0
-
MathOverflow: Mármint, valamiért Y tengelyről ki-be lépeget.. Nem vagyok benne biztos hogy mindent jól csináltam -e volna. 6 éve 0
 AlBundy
{ Polihisztor }
válasza
AlBundy
{ Polihisztor }
válasza
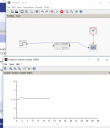
Nekem egyáltalán nem furcsa.  Látom, hogy módosítottad a paramétereket, a rendszermátrix immár
Látom, hogy módosítottad a paramétereket, a rendszermátrix immár
`A=[[0,1,0],[0,0,1],[-1000,-1,0]]`.
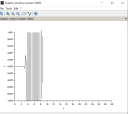
Ennek a sajátértékei `-9.97`, valamint `4.98 pm 8.69 j`. Az utóbbi két sajátérték a komplex számsík jobb felén helyezkedik el, tehát a rendszer nem stabil. Mivel a labilis sajátértékek komplex konjugált párok, az ugrásválasz egy exponenciálisan növekvő amplitúdójú lengés. Ezt látod a képen, csak nagyon bele van zoomolva.
Egyébként már az átviteli függvényből is látszik, hogy labilis, ha megnézed a pólusait (amelyek nem meglepő módon megegyeznek az állapotmátrix sajátértékeivel):
https://www.wolframalpha.com/input/?i=p%5E3%2Bp%2B1000%3D0
 Látom, hogy módosítottad a paramétereket, a rendszermátrix immár
Látom, hogy módosítottad a paramétereket, a rendszermátrix immár`A=[[0,1,0],[0,0,1],[-1000,-1,0]]`.
Ennek a sajátértékei `-9.97`, valamint `4.98 pm 8.69 j`. Az utóbbi két sajátérték a komplex számsík jobb felén helyezkedik el, tehát a rendszer nem stabil. Mivel a labilis sajátértékek komplex konjugált párok, az ugrásválasz egy exponenciálisan növekvő amplitúdójú lengés. Ezt látod a képen, csak nagyon bele van zoomolva.
Egyébként már az átviteli függvényből is látszik, hogy labilis, ha megnézed a pólusait (amelyek nem meglepő módon megegyeznek az állapotmátrix sajátértékeivel):
https://www.wolframalpha.com/input/?i=p%5E3%2Bp%2B1000%3D0
1
- Még nem érkezett komment!
 MathOverflow
válasza
MathOverflow
válasza
Köszönöm szépen! 
Kicsit próbáltam kicsinyíteni, átírva Ymin: -1 millió Ymax: +1 milliós-s értékekre. Így is hasonló
ábrázolás jön ki, viszont ha az egyes kiugrások csúcsaira fókuszálok akkor talán látom hogy igazából nem levágás, mert picit különböznek a magasságaik. De csak talán. Mert ha nem milliós, hanem billiárdos értékekre írom át az Ymin/Ymax paramétert, akkor is hasonlóképpen alakulnak.
Mert ha nem milliós, hanem billiárdos értékekre írom át az Ymin/Ymax paramétert, akkor is hasonlóképpen alakulnak.
Vagy horizontális zoomra gondoltál? Akkor a refresh periodot kellene még kisebbre állítanom talán.
Köszönöm a részletes segítségeket!

Kicsit próbáltam kicsinyíteni, átírva Ymin: -1 millió Ymax: +1 milliós-s értékekre. Így is hasonló
ábrázolás jön ki, viszont ha az egyes kiugrások csúcsaira fókuszálok akkor talán látom hogy igazából nem levágás, mert picit különböznek a magasságaik. De csak talán.
 Mert ha nem milliós, hanem billiárdos értékekre írom át az Ymin/Ymax paramétert, akkor is hasonlóképpen alakulnak.
Mert ha nem milliós, hanem billiárdos értékekre írom át az Ymin/Ymax paramétert, akkor is hasonlóképpen alakulnak.Vagy horizontális zoomra gondoltál? Akkor a refresh periodot kellene még kisebbre állítanom talán.
Köszönöm a részletes segítségeket!

Módosítva: 6 éve
0
-
MathOverflow: (valahogy sikerult kitorolnom veletlen az elozo valaszomat..
 )
6 éve
0
)
6 éve
0
 AlBundy
{ Polihisztor }
válasza
AlBundy
{ Polihisztor }
válasza
Ez azért van, mert ugye a jel amplitúdója exponenciálisan nő, tehát gyakorlatilag nem tudsz annyira kizoomolni, hogy az elejét is lásd. Tessék, meganimáltam neked, hogyan változik a kimenet az első öt másodpercben, adaptív tengelyekkel:
https://imgur.com/a/ZB2AKtw
https://imgur.com/a/ZB2AKtw
1
-
MathOverflow: Nagyon köszönöm a segítségét, nagyon hasznos volt !
 6 éve
0
6 éve
0