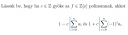Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Diszkrét Matematika, Témakör: Polinomok, Házi Feladat#2
 PikaPovWva
kérdése
PikaPovWva
kérdése
575
(Nem igazán világos ez a témakör. Igazából az egész Dimat homályos, ezért kérem a segítségeteket.)
Jelenleg 1 felhasználó nézi ezt a kérdést.
Dimat, diszkrét, Matematika, polinom
Dimat, diszkrét, Matematika, polinom
0
Felsőoktatás / Matematika
Válaszok
1 bongolo
{
bongolo
{  }
megoldása
}
megoldása
`ℤ` az egész számokat jelenti.
`ℤ[x]` olyan polinomot jelent, aminek együtthatói egészek. Vagyis pl.
`f=3x^2+x-2`
Ez egy másodfokú polinom, mert `x` legnagyobb együtthatója 2.
(most nem ez az `f`, ez csak példa egy polinomra.)
Általánosságban az `n`-edfokú `f(x)` polinom így írható fel:
`f(x)=a_n·x^n+a_(n-1)·x^(n-1)+...+a_1·x+a_0=sum_(i=0)^n a_i·x^i`
Akkor mondjuk, hogy a `c` egész szám gyöke egy `f(x)` polinomnak, ha `f(c)=0`
Ha `c` gyöke `f`-nek, akkor az `f` polinomból ki lehet emelni `(x-c)`-t:
`f(x)=(x-c)·g(x)`
(Ha `f(x)` `n`-edfokú polinom volt, akkor `g(x)` `n-1`-edfokú.)
Ez a kiemelés dolog úgy is fogalmazható, hogy `f(x)`-nek osztója `x-c`.
Pl. az `x^2-1` polinomnak az `1` gyöke, ezért ki lehet belőle emelni `(x-1)`-et:
`f(x)=x^2-1=(x-1)·g(x)` ahol `g(x)=x+1`
`f(x)`-nek osztója `x-1`. Ezt az "osztója" dolgot úgy szoktuk írni, hogy `x-1 | f(x)`
`bb"Most pedig a feladat megoldása:"`
`f(x)` az eredeti `n`-edfokú polinom:
`f(x)=a_n·x^n+a_(n-1)·x^(n-1)+...+a_1·x+a_0=sum_(i=0)^n a_i·x^i`
A `c` szám gyöke a polinomnak:
`f(x)=(x-c)·g(x)`
(nem ismerjük `g(x)`-et, de mindegy is.)
Be kellene valamit látni a polinom tényezőiből alkotott `sum_(i=0)^n a_i` számról, vagyis az `a_n+a_(n-1)+...+a_1+a_0` öszegről.
Ha kicsit belegondolunk, rájövünk, hogy ez az összeg éppen az `f(1)` érték! Ugye látod?
`f(1)=sum_(i=0)^n a_i`
És már meg is van a megoldás:
Mivel `f(x)=(x-c)·g(x)`,
ezért `f(1)=(1-c)·g(1)`, vagyis `1-c` osztója `f(1)`-nek. Kész.
A másodikhoz pedig lásd be, hogy az a szumma éppen `f("-1")`, stb.
`ℤ[x]` olyan polinomot jelent, aminek együtthatói egészek. Vagyis pl.
`f=3x^2+x-2`
Ez egy másodfokú polinom, mert `x` legnagyobb együtthatója 2.
(most nem ez az `f`, ez csak példa egy polinomra.)
Általánosságban az `n`-edfokú `f(x)` polinom így írható fel:
`f(x)=a_n·x^n+a_(n-1)·x^(n-1)+...+a_1·x+a_0=sum_(i=0)^n a_i·x^i`
Akkor mondjuk, hogy a `c` egész szám gyöke egy `f(x)` polinomnak, ha `f(c)=0`
Ha `c` gyöke `f`-nek, akkor az `f` polinomból ki lehet emelni `(x-c)`-t:
`f(x)=(x-c)·g(x)`
(Ha `f(x)` `n`-edfokú polinom volt, akkor `g(x)` `n-1`-edfokú.)
Ez a kiemelés dolog úgy is fogalmazható, hogy `f(x)`-nek osztója `x-c`.
Pl. az `x^2-1` polinomnak az `1` gyöke, ezért ki lehet belőle emelni `(x-1)`-et:
`f(x)=x^2-1=(x-1)·g(x)` ahol `g(x)=x+1`
`f(x)`-nek osztója `x-1`. Ezt az "osztója" dolgot úgy szoktuk írni, hogy `x-1 | f(x)`
`bb"Most pedig a feladat megoldása:"`
`f(x)` az eredeti `n`-edfokú polinom:
`f(x)=a_n·x^n+a_(n-1)·x^(n-1)+...+a_1·x+a_0=sum_(i=0)^n a_i·x^i`
A `c` szám gyöke a polinomnak:
`f(x)=(x-c)·g(x)`
(nem ismerjük `g(x)`-et, de mindegy is.)
Be kellene valamit látni a polinom tényezőiből alkotott `sum_(i=0)^n a_i` számról, vagyis az `a_n+a_(n-1)+...+a_1+a_0` öszegről.
Ha kicsit belegondolunk, rájövünk, hogy ez az összeg éppen az `f(1)` érték! Ugye látod?
`f(1)=sum_(i=0)^n a_i`
És már meg is van a megoldás:
Mivel `f(x)=(x-c)·g(x)`,
ezért `f(1)=(1-c)·g(1)`, vagyis `1-c` osztója `f(1)`-nek. Kész.
A másodikhoz pedig lásd be, hogy az a szumma éppen `f("-1")`, stb.
Módosítva: 6 éve
1
-
PikaPovWva: Köszönöm!
 6 éve
0
6 éve
0