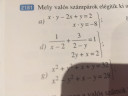Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matematika 10.osztály másodfokú egyenletrendszerek
 jl22
kérdése
jl22
kérdése
759
Sziasztok! A d) feladatrészhez szeretném segítségeteket kérni, meg úgy egyáltalán ehhez a feladattípushoz. Az elején elakadtam.:( Nagyon szépen köszönöm előre is!
Jelenleg 1 felhasználó nézi ezt a kérdést.
Egyenletrendszer
Egyenletrendszer
0
Középiskola / Matematika
Válaszok
2 Rantnad
{
Rantnad
{  }
megoldása
}
megoldása
d) A második egyenletből x=2-2y adódik, ezt beírjuk az első egyenleten x helyére:
1/(2-2y-2) + 3/(2-y) = 1, elvégezzük a kivonást:
-1/(2y) + 3/(2-y) = 1, szorzunk a nevezőkkel:
-1*(2-y) + 3*(2y) = 2y*(2-y), majd kibontjuk a zárójeleket:
y-2 + 6y = 4y-2y², itt a bal oldalt 0-ra redukáljuk:
0=-2y²-3y+2, lehet osztani (-1)-gyel:
0=2y²+3y-2, ezt többek között megoldóképlettel is meg lehet oldani:
y1;2=(-3±√ 3²-4*2*(-2) )/4=(-3±5)/4, tehát
y₁=1/2, y₂=-2. Mivel x=2-2y volt, ezért x₁=2-2*(1/2)=1, x₂=2-2*(-2)=6, ellenőrzés WolframaAlphával:
http://www.wolframalpha.com/input/?i=%7B+1%2F(x-2)+%2B+3%2F(2-y)+%3D+1+;+2y%2Bx%3D2+%7D
Tehát jól számoltunk, persze manuálisan is lehet ellenőrizni.
1/(2-2y-2) + 3/(2-y) = 1, elvégezzük a kivonást:
-1/(2y) + 3/(2-y) = 1, szorzunk a nevezőkkel:
-1*(2-y) + 3*(2y) = 2y*(2-y), majd kibontjuk a zárójeleket:
y-2 + 6y = 4y-2y², itt a bal oldalt 0-ra redukáljuk:
0=-2y²-3y+2, lehet osztani (-1)-gyel:
0=2y²+3y-2, ezt többek között megoldóképlettel is meg lehet oldani:
y1;2=(-3±√ 3²-4*2*(-2) )/4=(-3±5)/4, tehát
y₁=1/2, y₂=-2. Mivel x=2-2y volt, ezért x₁=2-2*(1/2)=1, x₂=2-2*(-2)=6, ellenőrzés WolframaAlphával:
http://www.wolframalpha.com/input/?i=%7B+1%2F(x-2)+%2B+3%2F(2-y)+%3D+1+;+2y%2Bx%3D2+%7D
Tehát jól számoltunk, persze manuálisan is lehet ellenőrizni.
1
-
jl22: Köszönöm szépen!
 9 éve
0
9 éve
0
 Benczusch
válasza
Benczusch
válasza
Kikötések: mivel nevezőben nem lehet 0:
x-2 ≠ 0 ⇒ x ≠ 2
2-y ≠ 0 ⇒ y ≠ 2
A második egyenletből kifejezzük x-et:
x = 2 - 2y
Ezt behelyettesítjük az első egyenletbe:
1 / (2 - 2y) - 2 + 3 / 2 - y = -1 / 2y + 3 / 2 - y = 1
Mindkét oldalt megszorozhatjuk 2 * y * (2 - y)-nal. (Ez azért jó nekünk, mert a 2y a bal, a (2 - y) a jobb oldali összeadandó nevezőjét tünteti el.)
-(2 - y) * 2y/2y + 3 * 2y * 2 - y / 2 - y = 2 * y * (2 - y)
-2 + y + 6y = 4y - 2 y2
Nullára rendezzük a jobb oldalt:
2 y2+3y-2 = 0
Másodfokú egyenlet megoldóképlete
D = b2-4ac = 32 - 4 * 2 * (-2) = 25
y1= -b + √ D / 2 * a = -3 + √ 25 / 2 * 2 = 0,5
y2= -b - √ D / 2 * a = -3 - √ 25 / 2 * 2 = -2
Korábban felhasználtuk az x = 2 - 2y helyettesítést, ezalapján:
x1 = 2 - 2y1= 1
x2 = 2 - 2y2= 6
Ellenőrizzük a kikötéseket mindenre (x1, x2,y1, y2 közül egyik se lehet 2), nincs semmi ütközés, úgyhogy mindkét számpár kielégíti:
x1 = 1; y1 =0,5
x2 = 6; y2 =-2
(Behelyettesítéssel ellenőrzünk)
x-2 ≠ 0 ⇒ x ≠ 2
2-y ≠ 0 ⇒ y ≠ 2
A második egyenletből kifejezzük x-et:
x = 2 - 2y
Ezt behelyettesítjük az első egyenletbe:
1 / (2 - 2y) - 2 + 3 / 2 - y = -1 / 2y + 3 / 2 - y = 1
Mindkét oldalt megszorozhatjuk 2 * y * (2 - y)-nal. (Ez azért jó nekünk, mert a 2y a bal, a (2 - y) a jobb oldali összeadandó nevezőjét tünteti el.)
-(2 - y) * 2y/2y + 3 * 2y * 2 - y / 2 - y = 2 * y * (2 - y)
-2 + y + 6y = 4y - 2 y2
Nullára rendezzük a jobb oldalt:
2 y2+3y-2 = 0
Másodfokú egyenlet megoldóképlete
D = b2-4ac = 32 - 4 * 2 * (-2) = 25
y1= -b + √ D / 2 * a = -3 + √ 25 / 2 * 2 = 0,5
y2= -b - √ D / 2 * a = -3 - √ 25 / 2 * 2 = -2
Korábban felhasználtuk az x = 2 - 2y helyettesítést, ezalapján:
x1 = 2 - 2y1= 1
x2 = 2 - 2y2= 6
Ellenőrizzük a kikötéseket mindenre (x1, x2,y1, y2 közül egyik se lehet 2), nincs semmi ütközés, úgyhogy mindkét számpár kielégíti:
x1 = 1; y1 =0,5
x2 = 6; y2 =-2
(Behelyettesítéssel ellenőrzünk)
1
- Még nem érkezett komment!