A megoldásom így néz ki a füzetemben de nem értem...

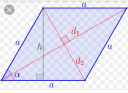
A paralelogramma területének a fele! Az egyenlő szárú háromszög!
A paralelogramma területe=
a×h=T
h=a×sin(alfa) !!
T=sin(alfa)×a2
A háromszög területe: T∆=T/2
T∆=(Sin(alfa)×a2)/2

A feladatot többféleképp meg lehet oldani. Ha kérdező ismeri, a koszinusz-tétellel egységes, szép megoldás adható.

Legyen
A, B, C - a háromszög csúcsai
O - körülírt kör középpontja, ami a szimmetria tengelyen helyezkedik el, a csúcsoktól azonos távolságra.
T = 80 - háromszög területe
α = 42° - a háromszög szárszöge
a = ? - a háromszög alapja
b = ? - a háromszög szárai
R = ? - a háromszög körülírt körének sugara

A szár hossza a trigonometrikus területképletből
T = b²*sinα/2
b² = 2T/sinα --> b

A háromszög alapja (koszinusz-tétel)
a² = 2b²(1 - cosα) --> a

A körülírt kör sugara (koszinusz-tétel a BCO háromszögben)
b² = 2R²[1 - cos(180 - α)]
b² = 2R²(1 + cosα)
R² = 2b²/(1 + cosα) --> R

A 'b²' értéke megjelenik az első egyenletben, fel lehet használni a másik kettőben.

Ezzel minden kérdésre megadtuk a választ.