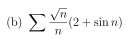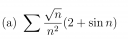Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Az alábbi sorokat ,hogyan vizsgálnátok meg konvergencia szempontjából?
asdasdasd
kérdése
335
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1
bongolo
{ 
}
megoldása
Tudjuk, hogy `sum 1/n^p` konvergens, ha `p > 1` és divergens, ha `p ≤ 1`.
b)
Minoráns kritérium:
`a_n=sqrtn/n(2+sin n)=(2+sin n)/n^(0.5) ≥ b_n=1/n^(0.5)`
És tudjuk, hogy `sum b_n` divergens.
a)
Majoráns kritérium:
`a_n=sqrtn/n^2(2+sin n)=(2+sin n)/n^(1.5) ≤ b_n = 3/n^(1.5) = 3/n^(0.1)·1/n^(1.4)`
és ha `3/n^(0.1) < 1`
vagyis `n > 3^(10)`,
akkor ` b_n < c_n=1/n^(1.4)`
És tudjuk, hogy `sum c_n` konvergens.
b)
Minoráns kritérium:
`a_n=sqrtn/n(2+sin n)=(2+sin n)/n^(0.5) ≥ b_n=1/n^(0.5)`
És tudjuk, hogy `sum b_n` divergens.
a)
Majoráns kritérium:
`a_n=sqrtn/n^2(2+sin n)=(2+sin n)/n^(1.5) ≤ b_n = 3/n^(1.5) = 3/n^(0.1)·1/n^(1.4)`
és ha `3/n^(0.1) < 1`
vagyis `n > 3^(10)`,
akkor ` b_n < c_n=1/n^(1.4)`
És tudjuk, hogy `sum c_n` konvergens.
0
-
asdasdasd: Köszönöm a segítséged! Azonban ha nem gond akkor úgy is meg tudnád oldani,hogy a feladat határértékéből indulsz ki ? :/ (sajno ezeket a kritériumokat még nem vettük,mi határértékekkel oldjuk meg) 5 éve 0
-
bongolo: Nem lehet kiindulni a határértékből, mert divergens (az egyik). Szerintem tanultátok ezeket a kritériumokat. 5 éve 0
-
bongolo: A konvergensnek a határértéke a Wolfram szerint valami nagyon durva kifejezés, tuti, hogy nem kell meghatározni. Csak azt kell, hogy konvergens. Az meg majoráns kritériummal megy. 5 éve 0