Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Három kör
 DeeDee
kérdése
DeeDee
kérdése
2162
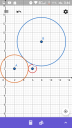
Van három különböző sugarú, egymást páronként érintő kör.
Mekkora a körök sugara, ha középpontjaik távolsága adott?
Haladóknak
1.) Mekkora a köröket kivülről érintő kör sugara?
2.) Mekkorák a páronkénti közös külső érintők meghúzásával keletkező háromszög oldalai?
Mekkora a körök sugara, ha középpontjaik távolsága adott?
Haladóknak
1.) Mekkora a köröket kivülről érintő kör sugara?
2.) Mekkorák a páronkénti közös külső érintők meghúzásával keletkező háromszög oldalai?
Jelenleg 1 felhasználó nézi ezt a kérdést.
1
Középiskola / Matematika
Válaszok
3 DomahidiPéter
megoldása
DomahidiPéter
megoldása
Most még csak az elsôt tudom megválaszolni..
Legyen A ,B, C; a körök sugarai.
X ,Y ,Z; a kör középppntjainak távolsága.
Ekkor
A+B=X B+C=Y. C+A=Z
Azonosságok:
B=X-A és C=Z-A
Y=B+C=(X-A)+(Z-A)=X+Z-2A
Y=X+Z-2A
Y+2A=X+Z
2A=X-Y+Z
A=0.5×(+X-Y+Z)
És ebből kiszámolható az összes oldal nagysága.
Legyen A ,B, C; a körök sugarai.
X ,Y ,Z; a kör középppntjainak távolsága.
Ekkor
A+B=X B+C=Y. C+A=Z
Azonosságok:
B=X-A és C=Z-A
Y=B+C=(X-A)+(Z-A)=X+Z-2A
Y=X+Z-2A
Y+2A=X+Z
2A=X-Y+Z
A=0.5×(+X-Y+Z)
És ebből kiszámolható az összes oldal nagysága.
Módosítva: 6 éve
0
-
DeeDee: Langyos, langyos... Fussál neki mégegyszer. :-) Nem tudnál egy rajzot mellékelni? És felejsd már el a nagybetűs írást. 6 éve 1
 DeeDee
válasza
DeeDee
válasza
Mivel úgy tűnik, a tieden kivül más megoldás nem várható, megmutatom a saját megoldásomat. Mikor a feladatot kiírtam, azt hittem, ez lesz a legkönnyebb...
Köszi rajzot, de én más értelmezéssel fogom használni.
Legyen
A, B, C egy háromszög három csúcsa
és
BC = a
CA = b
AB = c
a háromszög oldalai
ra, rb, rc - az A, B, C középpontú körök sugara
A feladat
a, b, c - adott
ra, rb, rc = ?
Elemezve az ábrát hamar kiderül, hogy a háromszög minden oldala két sugár összege, vagyis
1.) a = rb + rc
2.) b = rc + ra
3.) c = ra + rb
Van három egyenletünk a három ismeretlenhez, elvileg a feladat megoldható.
Mit tesz ilyenkor a gyerek?
Leszegett fejjel nekiáll a favágásnak: kifejezem, majd behelyettesítem... stb., anélkül, hogy gondolkodna, elemezne. Szó se róla, így is lehet, de itt minek? Mintha az lenne az alapelv, hogy miért egyszerűen, mikor bonyolultan is lehet.
Szóval kell egy jó ötlet. Mi lenne, ha...
Adjuk össze a három egyenletet
a + b + c = 2(ra + rb + rc)
A bal oldal a háromszög kerülete
K = 2(ra + rb + rc)
Bevezetve az 's' félkerületet
2s = 2(ra + rb + rc)
Egyszerűsítés után
4.) s = ra + rb + rc
Ezek után az ismeretlen sugarak
4.)-ből
ra = s - (rb + rc)
A zárójeles mennyiség az 1.) szerint az 'a' oldallal egyenlő, ezért
ra = s - a
Ennek mintájára a 2.) ill. 3.) egyenletet figyelembe véve
rb = s - b
rc = s - c
A feladat megoldva. :-)
Köszi rajzot, de én más értelmezéssel fogom használni.
Legyen
A, B, C egy háromszög három csúcsa
és
BC = a
CA = b
AB = c
a háromszög oldalai
ra, rb, rc - az A, B, C középpontú körök sugara
A feladat
a, b, c - adott
ra, rb, rc = ?
Elemezve az ábrát hamar kiderül, hogy a háromszög minden oldala két sugár összege, vagyis
1.) a = rb + rc
2.) b = rc + ra
3.) c = ra + rb
Van három egyenletünk a három ismeretlenhez, elvileg a feladat megoldható.
Mit tesz ilyenkor a gyerek?
Leszegett fejjel nekiáll a favágásnak: kifejezem, majd behelyettesítem... stb., anélkül, hogy gondolkodna, elemezne. Szó se róla, így is lehet, de itt minek? Mintha az lenne az alapelv, hogy miért egyszerűen, mikor bonyolultan is lehet.
Szóval kell egy jó ötlet. Mi lenne, ha...
Adjuk össze a három egyenletet
a + b + c = 2(ra + rb + rc)
A bal oldal a háromszög kerülete
K = 2(ra + rb + rc)
Bevezetve az 's' félkerületet
2s = 2(ra + rb + rc)
Egyszerűsítés után
4.) s = ra + rb + rc
Ezek után az ismeretlen sugarak
4.)-ből
ra = s - (rb + rc)
A zárójeles mennyiség az 1.) szerint az 'a' oldallal egyenlő, ezért
ra = s - a
Ennek mintájára a 2.) ill. 3.) egyenletet figyelembe véve
rb = s - b
rc = s - c
A feladat megoldva. :-)
0
- Még nem érkezett komment!