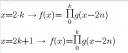Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Függvényegyenlet (2)
 gyula205
kérdése
gyula205
kérdése
583
Van-e megoldása az F(x+2) = (x²+3x+1)·F(x) függvényegyenletnek, ahol F(x) folytonos és F(0) =1?
Jelenleg 1 felhasználó nézi ezt a kérdést.
1
Felsőoktatás / Matematika
Válaszok
4 DomahidiPéter
válasza
DomahidiPéter
válasza
F(x+2) = (x²+3x+1)·F(x)
Vezessünk be egy G(x) függvényt.
G(x)=x²+3x+1
Ezért
F(x+2)=G(x)·F(x)
F(x)=G(x-2)·F(x-2)
F(x-2)=G(x-4)·F(x-4)
F(x)=G(x)×G(x-2)×G(x-4)....G(x-2k).
Ez a sorozat nem konvergens.. Tehát nincs "megoldás"
Vezessünk be egy G(x) függvényt.
G(x)=x²+3x+1
Ezért
F(x+2)=G(x)·F(x)
F(x)=G(x-2)·F(x-2)
F(x-2)=G(x-4)·F(x-4)
F(x)=G(x)×G(x-2)×G(x-4)....G(x-2k).
Ez a sorozat nem konvergens.. Tehát nincs "megoldás"
0
-
gyula205: Inkább F(x)=G(x)×G(x-2)×G(x-4)....G(x-2k)F(x-2k). De mi van a konvergenciával? 7 éve 1
-
DomahidiPéter: Nem konvergens.. Hanem divergens.. Tehát ilyen függvény nincs 7 éve 0
-
bongolo: Ez akkor lenne jó megoldás, ha `lim_(k->∞) F(x-2k) = 1` lenne, illetve ha `x-2k` a nullához tartana. De nem oda tart. 7 éve 0
-
DomahidiPéter: Hát igen.. Ilyen függvény nincs sajnos.. 7 éve 0
-
bongolo: De, van, mert le tud állni a rekurzió a nulla körül. Olvasd el a válaszomat. 7 éve 0
 bongolo
{
bongolo
{  }
megoldása
}
megoldása
Van ilyen függvény.
Nézzük, mit tudunk `f()`-ről:
Legyen most is `g(x)=x^2+3x+1`
Ha ismernénk a `0 ≤ x < 2` tartományban `f(x)` értékeit, akkor:
- pozitív számoknál az `f(x)=g(x-2)·f(x-2)` sorozat használható, hogy `x`-ről leérjünk az ismert tartományhoz, ahol leáll a rekurzió
- negatív számoknál pedig az `f(x)=f(x+2)/g(x)`, de csak akkor, ha `g(x)≠0` egyik lépésnél sem.
Néhány helyen tudjuk a pontos értéket:
a) Páros számoknál `f(0)=1` miatt:
- Ha `x=2n, n ∈ ℤ: f(x)=prod_(k=1)^n g(2k-2)`
- Ha `x=-2n, n ∈ ℤ: f(x)=prod_(k=1)^n 1/(g(-2k))`
Speciálisan `f(2)=g(0)=1` (és persze `f(0)=1` is ismert)
b) Ahol `g(x)=0` valamelyik lépésben:
`g(x)` gyökei ezek:
`x_"1,2"=(-3+-sqrt(5))/2`
Ezek nagyjából -0.38197 és -2.6180. "Szerencsére" ezek nem páros számok, ezért nem ütközik össze ez az előző esettel, továbbra is jók az a) kikötések.
Legyen `ξ_1=x_2+4=(5-sqrt(5))/2`
és `qquad ξ_2=x_1+2=(1+sqrt(5))/2`
Ezek a `[0,2)` tartományban vannak, `ξ_1 < ξ_2`.
Tudjuk, hogy `f(x_1)=f(x_2)=f(ξ_1)=f(ξ_2)=0`, általánosabban, `r={1,2}`, `ξ_r` jelöléssel mindkét `ξ`-re:
- Ha `x=ξ_r+2n, n ∈ ℕ: f(x)=0`
Van tehát 3 fix pontunk a `[0, 2)` intervallumon: `f(0)=1, f(ξ_1)=0, f(ξ_2)=0`
A többi `f(x), x ∈ (0, 2)\ \\ \ ξ_r` esetén tetszőleges folytonos függvény jó lesz, pl az, ahol egyenes vonalakkal kötjük össze a
`(0,f(0)) -> (ξ_1,f(ξ_1)) -> (ξ_2,f(ξ_2)) -> (2,1)`
pontokat (ilyenkor a `[ξ_1, ξ_2]` intervallumon minden `f(x)=0`, de ez nem szükségszerű). Végtelen sok más is elképzelhető. (Van olyan is, ami nem csak folytonos, hanem N-szer deriválható. Lehet, hogy van olyan is, ami végtelen sokszor deriválható.)
Nevezzük ezt a `[0,2]` intervallumon definiált függvényt `φ(x)`-nek, ezzel `f(x)` kifejezhető:
- Ha `x ≥ 0, n=⌊x/2⌋: f(x)=φ(x-2n) · prod_(k=1)^n g(x-2k)`
- Ha `x < 0, n=-⌊x/2⌋: f(x)=φ(x+2n) · prod_(k=1)^n 1/(g(x+2k-2))`
(... Remélem nem rontottam el itt a végén a plusz-mínuszt, meg az `n`-t, meg hogy `k` meddig is megy, ellenőrizd le néhány `x`-re.)
(`bb"EDIT:"` Bizony elrontottam: `g(x-2k-2)`-t írtam a pozitív `x`-eknél, pedig `g(x-2k)` kell. Javítva. Bocs.)
Könnyen bizonyítható, hogy az így definiált függvény folytonos.
Nézzük, mit tudunk `f()`-ről:
Legyen most is `g(x)=x^2+3x+1`
Ha ismernénk a `0 ≤ x < 2` tartományban `f(x)` értékeit, akkor:
- pozitív számoknál az `f(x)=g(x-2)·f(x-2)` sorozat használható, hogy `x`-ről leérjünk az ismert tartományhoz, ahol leáll a rekurzió
- negatív számoknál pedig az `f(x)=f(x+2)/g(x)`, de csak akkor, ha `g(x)≠0` egyik lépésnél sem.
Néhány helyen tudjuk a pontos értéket:
a) Páros számoknál `f(0)=1` miatt:
- Ha `x=2n, n ∈ ℤ: f(x)=prod_(k=1)^n g(2k-2)`
- Ha `x=-2n, n ∈ ℤ: f(x)=prod_(k=1)^n 1/(g(-2k))`
Speciálisan `f(2)=g(0)=1` (és persze `f(0)=1` is ismert)
b) Ahol `g(x)=0` valamelyik lépésben:
`g(x)` gyökei ezek:
`x_"1,2"=(-3+-sqrt(5))/2`
Ezek nagyjából -0.38197 és -2.6180. "Szerencsére" ezek nem páros számok, ezért nem ütközik össze ez az előző esettel, továbbra is jók az a) kikötések.
Legyen `ξ_1=x_2+4=(5-sqrt(5))/2`
és `qquad ξ_2=x_1+2=(1+sqrt(5))/2`
Ezek a `[0,2)` tartományban vannak, `ξ_1 < ξ_2`.
Tudjuk, hogy `f(x_1)=f(x_2)=f(ξ_1)=f(ξ_2)=0`, általánosabban, `r={1,2}`, `ξ_r` jelöléssel mindkét `ξ`-re:
- Ha `x=ξ_r+2n, n ∈ ℕ: f(x)=0`
Van tehát 3 fix pontunk a `[0, 2)` intervallumon: `f(0)=1, f(ξ_1)=0, f(ξ_2)=0`
A többi `f(x), x ∈ (0, 2)\ \\ \ ξ_r` esetén tetszőleges folytonos függvény jó lesz, pl az, ahol egyenes vonalakkal kötjük össze a
`(0,f(0)) -> (ξ_1,f(ξ_1)) -> (ξ_2,f(ξ_2)) -> (2,1)`
pontokat (ilyenkor a `[ξ_1, ξ_2]` intervallumon minden `f(x)=0`, de ez nem szükségszerű). Végtelen sok más is elképzelhető. (Van olyan is, ami nem csak folytonos, hanem N-szer deriválható. Lehet, hogy van olyan is, ami végtelen sokszor deriválható.)
Nevezzük ezt a `[0,2]` intervallumon definiált függvényt `φ(x)`-nek, ezzel `f(x)` kifejezhető:
- Ha `x ≥ 0, n=⌊x/2⌋: f(x)=φ(x-2n) · prod_(k=1)^n g(x-2k)`
- Ha `x < 0, n=-⌊x/2⌋: f(x)=φ(x+2n) · prod_(k=1)^n 1/(g(x+2k-2))`
(... Remélem nem rontottam el itt a végén a plusz-mínuszt, meg az `n`-t, meg hogy `k` meddig is megy, ellenőrizd le néhány `x`-re.)
(`bb"EDIT:"` Bizony elrontottam: `g(x-2k-2)`-t írtam a pozitív `x`-eknél, pedig `g(x-2k)` kell. Javítva. Bocs.)
Könnyen bizonyítható, hogy az így definiált függvény folytonos.
Módosítva: 7 éve
1
-
gyula205: x = ξ r + 2 n inkább az x=xr+2n képlettel számoltam volna. Nagyobb gondom az, hogyaz egyenes vonalak összekötésével származtatott 7 éve 0
-
gyula205: φ (fi) függvénnyel mit szeretnél elérni? 7 éve 0
-
bongolo: `x_r`-rel nem jó, mert az [1,2) tartományban kell lennie, azok meg nem ott vannak. A φ() függvény pont az, egy folytonos függvény azon az intervallumon, ez állítja le a rekurziót. 7 éve 0
-
gyula205: Miért akarod a rekurziót leállítani. Mindig csak a folytonosság van említve, az eredeti függvényegyenlettel mi történik, különösen az értelmezési tartomány tetsz. helyén? 7 éve 0
-
bongolo: Ha nincs leállítva a rekurzió, akkor van az, amit DomahidiPeter írt, hogy MINDEN nem páros x pontban elszáll a végtelenbe az érték, ezért leállítás nélkül nem létezne ilyen fv. 7 éve 0
-
gyula205: x>=0 x=1,5 esetén (n az x/2 alsó egésze) n=0, a produktum k=1-től 0-ig 7 éve 0
-
gyula205: szólna, ami ellentmondás. 7 éve 0
-
gyula205: Még mindig nem látom, hogy az általad definiált f(x) függvények miért elégítik ki a függvényegyenletet? 7 éve 0
-
bongolo: Nem ellentmondás, mert a product értéke definíció szerint 1, ha a kezdő érték nagyobb, mint a végső. 7 éve 0
-
bongolo: Sajnálom, hogy nem látod, hogyan működik az f(x), nézd meg jobban. 7 éve 0
-
bongolo: Írd fel, hogy mi az f(x) mondjuk x=3-nál, és hogy mi az f(x+2), és hogy tényleg f(x+2) = (x²+3x+1)·f(x) -e. 7 éve 0
-
bongolo: Meg mondjuk x=-3-nál is. 7 éve 0
-
gyula205: Nem egy tétel bizonyításnál találkoztam azzal az elvvel, hogy produktumnál és/vagy szummánál a kezdő érték mindig kisebb mint az index aktuális értéke. Amit leírtál a produktumról az számomra elfogadhatatlan. 7 éve 0
-
gyula205: Ha x=1,5, akkor f(x)=φ(x)g(x-4)=0, f(x+2)=φ(x+2)g(x-2)=φ(3,5)g(-0,5)-nél hogy számolod ki a φ(3,5)-öt, amikor [0,2) intervallumra vagyunk leszorítva? Ezen az intervallumon kivül a φ értéke mennyi? 7 éve 0
-
gyula205: Ha x=3, akkor n=1 és f(x)=φ(x-2)g(x-4)=φ(1)g(-1)=-1, f(x+2)=φ(x)g(x-2)=φ(3)g(1)=φ(3)5-nél hogyan számolod ki a φ(3)-at? 7 éve 0
-
bongolo: Olvasd mär el rendesen, ami oda van írva: Nem φ(x), hanem φ(x−2n). 7 éve 0
-
bongolo: A prod-ot meg mindenki így definiálja, hiába elfogadhatatlan ez neked. Lásd pl. https://www.wolframalpha.com/input/?i=prod_(k%3D1)%5E0+1234 Azért így definiálják, mert így kevesebb kivétellel kell számolni. De ha nem tetszik, alakítsd át úgy, hogy nem 2 definíciót adsz, hanem hármat. Nem nagy ördöngősség az se. 7 éve 0
-
gyula205: Ha x=-3, akkor n=1 esetén f(x)=φ(x+2)/g(x) és f(x+2)=φ(x+4)/g(x+2). f(-3)=φ(-1)/g(-3). Szintén előjön φ(-1) kiszámolási problémája. 7 éve 0
-
bongolo: Ha x=-3, akkor x/2=-1.5, alsó egész része -2, tehát n=2. Nem 1! f(-3)=φ(-3+2·2)·prod stb, vagyis φ(1) jön elő, nem φ(-1)! 7 éve 0
-
bongolo: Ezekkel nincs gond, x₁ és x₂ környékén a folytonossággal lehet probléma, arról majd írok részletesebben, ha ráérek kicsit később. 7 éve 0
-
bongolo: ost látom, hogy az f(x+2)-t is rosszul próbálod értelmezni: Az x+2 nem csak az f()-nél jön be, hanem az egész sorban mindenhol x helyett x+2-t kell gondolni, tehát ha x+2 < 0, n=-[(x+2)/2] stb. Máshogy fogalmazva: mondjuk x=-5 esetén f(-3) értékét kell kiszámolni. 7 éve 0
-
gyula205: x=-3-nál kijött g(-3)f(-3)=f(-1), viszont az x=3-nál f(5)=g(5-6)f(3). g(3)-at várok és kapom a g(-1)-et. 7 éve 0
-
gyula205: Vigyázat https://www.wolframalpha.com/input/?i=prod_(k%3D1)%5E0+1234 link nem egy hivatalos definició. A wolframalpha csalóka tud lenni néhány esetben, majd erre is fogok példát mutatni. 7 éve 0
-
bongolo: Bizony elrontottam: `g(x-2k-2)`-t írtam a pozitív `x`-eknél, pedig `g(x-2k)` kell. Javítva. Bocs. 7 éve 0
 DomahidiPéter
válasza
DomahidiPéter
válasza
Én egy ilyet találtam...
Módosítva: 7 éve
0
-
bongolo: A páratlan így önmagában nem jó, mert miért lenne f(1)=1 ? 7 éve 0
 bongolo
{
bongolo
{  }
válasza
}
válasza
Van probléma a megoldásommal: Lazán vettem, hogy "könnyen bizonyítható, hogy az így definiált függvény folytonos". Kicsit azért bonyolultabb, és kell is még hozzá néhány kikötés:
A `φ(x)` függvénytől annyit vártam el eddig:
- `φ(0)=φ(2)=0`
- `φ(ξ_1)=φ(ξ_2)=0`
- A `[0;2]` intervallumban folytonos.
Ennyi tényleg elég ahhoz, hogy a számegyenes majd egészében folytonos legyen az `f(x)`, de gondok vannak az `x_1` és `x_2` helyek környezetében, ahol `g(x)=0`! Ki van kerülve a nullával osztás azzal, hogy az `x=ξ_r+2n` pontokban mindenhol `f(x)=0` (ez az első kritérium az `f(x)` függvény definíciójában, bár a másik kettőtől kicsit messze van és nincs is benne `Π`, ezért el is felejti az ember...), de az nem elég. A folytonossághoz azt is biztosítani kell, hogy `lim_(x->ξ_r+2n) f(x)=0` legyen minden `r` és `n` esetén.
Könnyen belátható, hogy valójában probléma csak ezzel van:
`lim_(x->x_r) f(x)=0`
mindkét `r` esetén, hisz itt lenne nullával osztás. Nézzük, pontosan mi is van ezek körül:
a) `x_1 ≈ -0.38197` kis környezetében `n=1`, `f(x)` pedig:
`f_1(x)=(φ(x+2))/(g(x))`
Ahhoz, hogy `lim_(x->x_1)f_1(x)=0` legyen, az kell, hogy `φ(x+2)` ebben a kis tartományban a `g(x)`-nél gyorsabban tartson a nullához. Amit javasoltam (a három egyenes szakaszból álló `φ(x)`), az nem teljesíti ezt a feltételt, tehát nem jó. Van azért végtelen sok föggvény, ami jó lesz. De nézzük tovább:
b) `x_2 ≈ -2.6180` kis környezetében `n=2`, `f(x)` pedig:
`f_2(x)=(φ(x+4))/(g(x)·g(x+2))`
Ahhoz, hogy `lim_(x->x_2)f_2(x)=0` legyen, az kell, hogy `φ(x+4)` ebben a kis tartományban a `g(x)·g(x+2)`-nél gyorsabban tartson a nullához. A `g(x+2)` nem zavar, mert nem a 0-hoz tart (`g(x_2+2) ≈ -0.472136`), de a `g(x)` igen.
Tehát ezt a két kikötést is bele kell venni, hogy milyen `φ(x)` függvények a jók. Keressünk ilyen függvényt:
Ennek a "gyorsan nullához" tulajdonságnak csak az `x_1+2=ξ_2` és `x_2+4=ξ_1` kis környezetében kell teljesülnie, a többi helyen továbbra is lehet tetszőleges folytonos függvény, ami 0-ban és 2-ban 1 értéket vesz fel.
Elsőre direkt egy bonyolultabb függvényt mutatok:
Ha pl. a `ξ_2+-δ` tartományon belül ilyen a függvény:
- Ha `ξ_2-δ < x < ξ_2+δ`, akkor `φ(x)=g(x-2)·(x-ξ_2)`
Nézzük a limeszt:
`lim_(x->x_1) (φ(x+2))/(g(x))=lim_(x->x_1) (g(x)·(x+2-ξ_2))/(g(x))=x_1+2-ξ_2=0`
Tényleg nulla a határérték, teját `x_1`-ben folytonos az `f(x)`!
A `ξ_1+-δ` tartományon belül pedig mondjuk ilyen a függvény:
- Ha `ξ_1-δ < x < ξ_1+δ`, akkor `φ(x)=g(x-4)·(x-ξ_1)`
A limesz pedig:
`lim_(x->x_2) (φ(x+4))/(g(x)·g(x+2))=lim_(x->x_2) (g(x)·(x+4-ξ_1))/(g(x)·g(x+2))=(x_2+4-ξ_1)/(g(x_2+2))=0`
A többi `x`-en bármilyen folytonos függvény jó, ami a két szélen felmegy 1-be.
Mondok azért sokkal egyszerűbb függvényt is! Majdnem ugyanaz, mint amit az előző válaszomban mondtam:
Egyenes vonalakkal kötjük össze a `(0, 1) -> (ξ_1-δ, 0) -> (ξ_2+δ, 0) -> (2,1)` pontokat.
`δ` tetszőleges kicsi szám lehet.
Lehet persze kicsit nagyobb is a delta, amikor mondjuk így megy a három vonal:
`(0, 1) -> (0.1, 0) -> (1.9,0) -> (2,1)`
Ezek a kritikus tartományban olyan "gyorsan" közelítenek a nullához, hogy végig nullák
A `φ(x)` függvénytől annyit vártam el eddig:
- `φ(0)=φ(2)=0`
- `φ(ξ_1)=φ(ξ_2)=0`
- A `[0;2]` intervallumban folytonos.
Ennyi tényleg elég ahhoz, hogy a számegyenes majd egészében folytonos legyen az `f(x)`, de gondok vannak az `x_1` és `x_2` helyek környezetében, ahol `g(x)=0`! Ki van kerülve a nullával osztás azzal, hogy az `x=ξ_r+2n` pontokban mindenhol `f(x)=0` (ez az első kritérium az `f(x)` függvény definíciójában, bár a másik kettőtől kicsit messze van és nincs is benne `Π`, ezért el is felejti az ember...), de az nem elég. A folytonossághoz azt is biztosítani kell, hogy `lim_(x->ξ_r+2n) f(x)=0` legyen minden `r` és `n` esetén.
Könnyen belátható, hogy valójában probléma csak ezzel van:
`lim_(x->x_r) f(x)=0`
mindkét `r` esetén, hisz itt lenne nullával osztás. Nézzük, pontosan mi is van ezek körül:
a) `x_1 ≈ -0.38197` kis környezetében `n=1`, `f(x)` pedig:
`f_1(x)=(φ(x+2))/(g(x))`
Ahhoz, hogy `lim_(x->x_1)f_1(x)=0` legyen, az kell, hogy `φ(x+2)` ebben a kis tartományban a `g(x)`-nél gyorsabban tartson a nullához. Amit javasoltam (a három egyenes szakaszból álló `φ(x)`), az nem teljesíti ezt a feltételt, tehát nem jó. Van azért végtelen sok föggvény, ami jó lesz. De nézzük tovább:
b) `x_2 ≈ -2.6180` kis környezetében `n=2`, `f(x)` pedig:
`f_2(x)=(φ(x+4))/(g(x)·g(x+2))`
Ahhoz, hogy `lim_(x->x_2)f_2(x)=0` legyen, az kell, hogy `φ(x+4)` ebben a kis tartományban a `g(x)·g(x+2)`-nél gyorsabban tartson a nullához. A `g(x+2)` nem zavar, mert nem a 0-hoz tart (`g(x_2+2) ≈ -0.472136`), de a `g(x)` igen.
Tehát ezt a két kikötést is bele kell venni, hogy milyen `φ(x)` függvények a jók. Keressünk ilyen függvényt:
Ennek a "gyorsan nullához" tulajdonságnak csak az `x_1+2=ξ_2` és `x_2+4=ξ_1` kis környezetében kell teljesülnie, a többi helyen továbbra is lehet tetszőleges folytonos függvény, ami 0-ban és 2-ban 1 értéket vesz fel.
Elsőre direkt egy bonyolultabb függvényt mutatok:
Ha pl. a `ξ_2+-δ` tartományon belül ilyen a függvény:
- Ha `ξ_2-δ < x < ξ_2+δ`, akkor `φ(x)=g(x-2)·(x-ξ_2)`
Nézzük a limeszt:
`lim_(x->x_1) (φ(x+2))/(g(x))=lim_(x->x_1) (g(x)·(x+2-ξ_2))/(g(x))=x_1+2-ξ_2=0`
Tényleg nulla a határérték, teját `x_1`-ben folytonos az `f(x)`!
A `ξ_1+-δ` tartományon belül pedig mondjuk ilyen a függvény:
- Ha `ξ_1-δ < x < ξ_1+δ`, akkor `φ(x)=g(x-4)·(x-ξ_1)`
A limesz pedig:
`lim_(x->x_2) (φ(x+4))/(g(x)·g(x+2))=lim_(x->x_2) (g(x)·(x+4-ξ_1))/(g(x)·g(x+2))=(x_2+4-ξ_1)/(g(x_2+2))=0`
A többi `x`-en bármilyen folytonos függvény jó, ami a két szélen felmegy 1-be.
Mondok azért sokkal egyszerűbb függvényt is! Majdnem ugyanaz, mint amit az előző válaszomban mondtam:
Egyenes vonalakkal kötjük össze a `(0, 1) -> (ξ_1-δ, 0) -> (ξ_2+δ, 0) -> (2,1)` pontokat.
`δ` tetszőleges kicsi szám lehet.
Lehet persze kicsit nagyobb is a delta, amikor mondjuk így megy a három vonal:
`(0, 1) -> (0.1, 0) -> (1.9,0) -> (2,1)`
Ezek a kritikus tartományban olyan "gyorsan" közelítenek a nullához, hogy végig nullák

0
- Még nem érkezett komment!