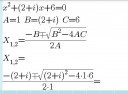Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Feladat
 Törölt
kérdése
Törölt
kérdése
506
Hali ! Valaki segítene megoldani ezt a feladatot a komplex számok halmazán
x²+(2+i)x+6=0
x²+(2+i)x+6=0
Jelenleg 1 felhasználó nézi ezt a kérdést.
feladat, matek
feladat, matek
0
Felsőoktatás / Matematika
Válaszok
3 DomahidiPéter
megoldása
DomahidiPéter
megoldása
Második
0
-
Rantnad: Nem, mintha kötözködni szeretnék, de ez így még nincs kész; a gyökvonást is el kell végezni. 7 éve 0
-
DomahidiPéter: Tivább vezeted ? 7 éve 0
-
Rantnad: Persze. 7 éve 1
 Rantnad
{
Rantnad
{  }
válasza
}
válasza
Maradjunk a √ 4i-21 alaknál, csak hogy egész számokkal számolhassunk.
Négyzetgyököt még könnyen tudunk algebrailag vonni, nem szükséges a trigonometrikus/exponenciális alak.
Tegyük fel, hogy a gyökvonás eredménye szintén komplex lesz, ekkor viszont felírható `a+bi` alakban, ahol `a;b` valós számok. Tehát:
√ 4i-21 `=a+bi`, négyzetre emelünk:
`4i-21 = a²+2abi-b²`
Két komplex szám akkor és csak akkor egyenlő egymással, hogyha a valós és képzetes részeik megegyeznek.
Valós részek: `-21 ; a²-b²`
Képzetes részek: `4 ; 2abi `
Tehát ezeket az egyenleteket kapjuk:
`-21 = a²-b²`
`4 = 2ab`
Ez egy egyenletrendszer, amit meg tudunk oldani. A második egyenletből `2/a=b` adódik, ezt visszaírjuk az első egyenletbe:
`-21 = a² - (2/a)²`, zárójelet bontunk és szorzunk `a²`-tel:
`-21*a² = a⁴ - 4`
Ez egy másodfokúra visszavezethető egyenlet, amelynek valós megoldásai kellenek. Ha ezek megvannak, akkor abból b értéke is meglesz, így megkapjuk azt a két számot, amelyeknek négyzete 4i-21.
Négyzetgyököt még könnyen tudunk algebrailag vonni, nem szükséges a trigonometrikus/exponenciális alak.
Tegyük fel, hogy a gyökvonás eredménye szintén komplex lesz, ekkor viszont felírható `a+bi` alakban, ahol `a;b` valós számok. Tehát:
√ 4i-21 `=a+bi`, négyzetre emelünk:
`4i-21 = a²+2abi-b²`
Két komplex szám akkor és csak akkor egyenlő egymással, hogyha a valós és képzetes részeik megegyeznek.
Valós részek: `-21 ; a²-b²`
Képzetes részek: `4 ; 2abi `
Tehát ezeket az egyenleteket kapjuk:
`-21 = a²-b²`
`4 = 2ab`
Ez egy egyenletrendszer, amit meg tudunk oldani. A második egyenletből `2/a=b` adódik, ezt visszaírjuk az első egyenletbe:
`-21 = a² - (2/a)²`, zárójelet bontunk és szorzunk `a²`-tel:
`-21*a² = a⁴ - 4`
Ez egy másodfokúra visszavezethető egyenlet, amelynek valós megoldásai kellenek. Ha ezek megvannak, akkor abból b értéke is meglesz, így megkapjuk azt a két számot, amelyeknek négyzete 4i-21.
Módosítva: 7 éve
1
- Még nem érkezett komment!