Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Kör egyenlete
 nemtudom99
kérdése
nemtudom99
kérdése
3371
Egy kör egyik átmérőjének végpontjai: A(-3; 2) és B(5; - 4). Írja fel ennek a körnek az egyenletét!
Jelenleg 1 felhasználó nézi ezt a kérdést.
#matek #kör #egyenlete
#matek #kör #egyenlete
0
Középiskola / Matematika
Válaszok
3 DomahidiPéter
megoldása
DomahidiPéter
megoldása
25={x-1}^2+{y+1}^2
Kell levezetés?
Kell levezetés?
2
-
nemtudom99: Az nagyon jó lenne, köszönöm! 7 éve 0
 DomahidiPéter
válasza
DomahidiPéter
válasza
Az a lényeg hogy meg kell határozni az A B szakasz hosszát..
AB/2 a kör sugara..
1 Két pont távolságának egyenlete:
A=(x,y). B=(x",y").
AB^2=(x-x")^2+(y-y")^2
Behelyettesítve:
A=(-3,2). És B=(5,-4)
AB^2=(-3-5)^2+(2-(-4))^2=(-8)^2+6^2=100
Ha AB^2=100 akkor AB=√100=10
A kör sugara egyenlő AB/2
R=5
2. Az AB szakasz felező pontja a kör közép pontja.
Itt a képlet a felező ponthoz..(jelöljük C-vel)
A={x,y} B={x",y"}
C={x-x",y-y"}×0.5+(x",y")
A={-3,2} B=(5,-4)
C={-3-5,2-(-4)}×0.5+(5,-4)=
{-8,6}×0.5+(5,-4)={-4,3}+(5,-4)=(1,-1)
Tehát a kör középpontja C={1,-1}
Egy C középpontú és R sugarú kör egyenlete:
C={u,v}
(X-u)^2+(Y+v)^2=R^2
Így tehát:
C={1,-1} R=5
(x-1)^2+(y-1)^2=5^2 (=25)
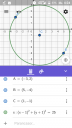
A képen a Gegebra nevű app ban ellenőriztem.. Érthető volt?
AB/2 a kör sugara..
1 Két pont távolságának egyenlete:
A=(x,y). B=(x",y").
AB^2=(x-x")^2+(y-y")^2
Behelyettesítve:
A=(-3,2). És B=(5,-4)
AB^2=(-3-5)^2+(2-(-4))^2=(-8)^2+6^2=100
Ha AB^2=100 akkor AB=√100=10
A kör sugara egyenlő AB/2
R=5
2. Az AB szakasz felező pontja a kör közép pontja.
Itt a képlet a felező ponthoz..(jelöljük C-vel)
A={x,y} B={x",y"}
C={x-x",y-y"}×0.5+(x",y")
A={-3,2} B=(5,-4)
C={-3-5,2-(-4)}×0.5+(5,-4)=
{-8,6}×0.5+(5,-4)={-4,3}+(5,-4)=(1,-1)
Tehát a kör középpontja C={1,-1}
Egy C középpontú és R sugarú kör egyenlete:
C={u,v}
(X-u)^2+(Y+v)^2=R^2
Így tehát:
C={1,-1} R=5
(x-1)^2+(y-1)^2=5^2 (=25)
A képen a Gegebra nevű app ban ellenőriztem.. Érthető volt?
0
- Még nem érkezett komment!