Gyakorlatilag igen.
Érdekel mélyebben is, hogy miért így jön ki?

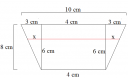
Vegyük a testnek az alaplapokra merőleges fősíkmetszetét (mintha képzeletben egy késsel félbevágnád a testet, és ami a vágással keletkezik, az a fősíkmetszet), ekkor egy húrtrapézt kapunk (mellékletben láthatod az ábrát); ennek alsó alaja 4 cm, felső alapja 10 cm, magassága 8 cm.
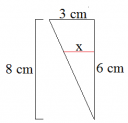
Most húzzunk be egy, az alapokkal párhozamos szakaszt, ami az alsó alaptól 6 cm távolságra van, és a belső magasságokat (2. ábra). Vegyük észre, hogy "két oldalt" keletkezet két-két derékszögű háromszög, egymásba tolva. Itt gyakorlatilag egy szögszár van elmetsze két párhuzamos szakasszal, tehát felírható a párhzamos szelők tétele; a hosszabbik szelőszakasz (10-4)/2=3 cm (csak úgy, ahogyan te gondolkodtál), így az ábrán kiolvasható adatok alapján, ha a rövidebbik szelőszakasz hossza x:
`6/x = 8/3`, ennek megoldása x=2,25, tehát a rövidebbik szelőszakasz ilyen hosszú. A másik oldalon szintén ez játszódik le.
Most jön az a része, amit te mondtál; ezeket a hosszokat hozzáadjuk a párhuzamos szakasz középső részéhez, ami 4 cm hosszú, így jön ki a 8,5 cm.
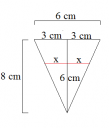
A te számítási módod attól más, hogy te nem külön-külön számoltad ki a kis piros szakaszok hosszát, hanem te fogtad ezt a két, egymásba ágyazott derékszöget, és összetoltad. Itt sajnos nem tudjuk használni a párhuzamos szelők tételét az egész háromszögre (mivel a szárszakaszok hossza ismeretlen), ellenben észrevesszük, hogy a két egymásba ágyazott egyenlő szárú háromszög hasonló (ezt viszont a tételre való hivatkozással megtehetjük), és a hasonlóság arányát is meg tudjuk határozni azok magasságaiból; λ=kicsi/nagy=3/4, így a piros szakasz hosszát úgy kapjuk, hogy a "fenti" oldalt megszorozzuk 3/4-del. Pont azt, amit te is csináltál.
Ha valami nem egyértelmű, kérdezz bátran!