Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Számítás ki az ABC háromszög területét????
 Ne3T
kérdése
Ne3T
kérdése
6028
A(2,3) B(-1,5) C(4,-1)
Ábrázoltam egy koordináta rendszerbe de nem tudom hogy számítsam ki a területet.
Ábrázoltam egy koordináta rendszerbe de nem tudom hogy számítsam ki a területet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
Matek, geometria
Matek, geometria
0
Középiskola / Matematika
Válaszok
3 Rantnad
{
Rantnad
{  }
válasza
}
válasza
Kellene tudni, hogy milyen számítási eljárásokról tanultál már.
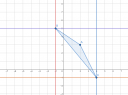
Ha lehet ábrázolni, és abból ki szabad olvasni a területet, akkor a következő dolgot tudod tenni; a háromszög csúcsain keresztül a koordináta-rendszer tengelyeivel párhuzamosan azokat az egyeneseket húzod be, amelyek a háromszöget nem metszik (adott esetben az oldalára eshet, az nem baj). Ha ezzel megvagy, akkor a mellékletben látható ábrát fogod kapni.
Ha a háromszög hegyesszögű lenne, akkor kicsit szerencsésebb helyzetben lennénk, mivel azt látnánk, hogy az egyenesek egy téglalapot fognak közre, amiből a háromszög oldalai 3 derékszögű háromszöget vágnak le, így ott csak annyi lenne a dolgunk, hogy kiszámolnánk a téglalap és a három derékszögű háromszög területét, majd ezeket egymásból kivonva kapnánk meg a kérdéses háromszög területét.
Itt sajnos még egy kicsit dolgoznunk kell; látható, hogy egy derékszögű háromszög megvan, azzal már tudunk mit kezdeni, ellenben a másik részen egy négyszög van. Ezt orvodolandó, az A pontból is indítunk két félegyenest (amelyek szintén nem metszik a háromszöget), ekkor a négyszögből keletkezik két derékszögű háromszög és egy téglalap (ami speciálisan most négyzet lesz).
A nagy téglalap területét ki tudjuk számolni, a három kisebb derékszögű háromszög területét szintén, a kis téglalap területéhez is van elég adat, így csak annyi a dolgunk, hogy ezeket kiszámoljuk, a nagy téglalap területéből kivonjuk az összes többiét, így az ABC háromszög területét kapjuk eredményül.
Ha tanultál már vektorokkal való számolást és trigonometriát (szinusz, koszinusz és társai), és azzal is szeretnéd látni a levezetést, szólj!
Ha lehet ábrázolni, és abból ki szabad olvasni a területet, akkor a következő dolgot tudod tenni; a háromszög csúcsain keresztül a koordináta-rendszer tengelyeivel párhuzamosan azokat az egyeneseket húzod be, amelyek a háromszöget nem metszik (adott esetben az oldalára eshet, az nem baj). Ha ezzel megvagy, akkor a mellékletben látható ábrát fogod kapni.
Ha a háromszög hegyesszögű lenne, akkor kicsit szerencsésebb helyzetben lennénk, mivel azt látnánk, hogy az egyenesek egy téglalapot fognak közre, amiből a háromszög oldalai 3 derékszögű háromszöget vágnak le, így ott csak annyi lenne a dolgunk, hogy kiszámolnánk a téglalap és a három derékszögű háromszög területét, majd ezeket egymásból kivonva kapnánk meg a kérdéses háromszög területét.
Itt sajnos még egy kicsit dolgoznunk kell; látható, hogy egy derékszögű háromszög megvan, azzal már tudunk mit kezdeni, ellenben a másik részen egy négyszög van. Ezt orvodolandó, az A pontból is indítunk két félegyenest (amelyek szintén nem metszik a háromszöget), ekkor a négyszögből keletkezik két derékszögű háromszög és egy téglalap (ami speciálisan most négyzet lesz).
A nagy téglalap területét ki tudjuk számolni, a három kisebb derékszögű háromszög területét szintén, a kis téglalap területéhez is van elég adat, így csak annyi a dolgunk, hogy ezeket kiszámoljuk, a nagy téglalap területéből kivonjuk az összes többiét, így az ABC háromszög területét kapjuk eredményül.
Ha tanultál már vektorokkal való számolást és trigonometriát (szinusz, koszinusz és társai), és azzal is szeretnéd látni a levezetést, szólj!
1
-
Ne3T: Persze tanultam, ha tudod légyszíves vezesd le úgy könnyebben megértem. 7 éve 0
 Rantnad
{
Rantnad
{  }
megoldása
}
megoldása
Ebben az esetben;
Először számoljuk ki az oldalak vektorait (mindegy, hogy merre mutatnak, illetve majdnem teljesen, ezt később látni fogjuk, miért);
AB→=(-3;2)
AC→=(2;-4)
BC→=(5;-6), remélem, ezt nem kell külön ecsetelnem. Ha mégis kellene, szólj.
Most adott három vektor, ezeknek a hosszát ki tudjuk számolni a tanult módon (de ezt is részletezem, ha szükséges):
|AB→|=√ (-3)²+2² =√ 13
|AC→|=√ 2²+(-4)² =√ 20
|BC→|=√ 5²+(-6)² =√ 61
Mindenképp szükségünk van a háromszög egyik szögére, innen két lehetőség van;
1) Skaláris szorzattal;
Válasszuk ki valamelyik szöget, amelyre fel akarjuk írni a skaláris szorzatot. És itt lényeges az, hogy a fenti vektorokat hogyan írtuk fel; nekünk olyan vektorok kellenek, amelyek a háromszög ugyanazon csúcsából indulnak, és, persze, a háromszög oldalára esnek. Ennek csak az AB→ és AC→ vektorok felelnek meg (természetesen ki lehet számolni a BA→, CA→ és CB→ vektorokat is, így akármelyik szöget választhatjuk), így válasszuk ezeket a vektorokat; ha a vektorok hajlásszöge α, akkor a skaláris szorzat:
(AB→)*(AC→) = |AB→|*|AC→|*cosα
A bal oldali szorzat így fog alakulni: (-3;2)*(2;-4)=(-3)*2+2*(-4)=-14
A jobb oldalon csak be kell helyettesíteni, így:
-14 = √ 13 * √ 20 * cosα, rendezés után ezt kapjuk:
`-14/(√(260)) = cosα`
Egyelőre hagyjuk így ezt az egyenletet, 2)-ben úgyis visszaköszön, majd ott folytatjuk.
2) Koszinusztétellel;
Azt már korábban megtanultuk, hogy ha egy háromszög minden oldala ismert, akkor felírható rá a koszinusztétel. Itt már nem lényeges a vektorok állása, csak a hosszuk kell, így a már tanult módon felírjuk; legyen szintén az A csúcsnál lévő α szög a kitüntetett, ekkor:
|BC→|² = |AB→|² + |AC→|² - 2*|AB→|*|AC→|*cosα
Behylettesítés után:
√ 61 ² = √ 13 ²+√ 20 ² - 2*√ 13 *√ 20 *cosα
Rendezés után a fenti egyenletet kapjuk, vagyis:
`-14/(√(260)) = cosα`
Itt szintén két lehetőség van; az egyik, hogy kiszámoljuk az α szög nagyságát, és azzal számolunk tovább. Ezzel csak annyi a probléma, hogy mindenképp egy kerekített értékkel kellene továbbszámolnunk, így az eredmény is csak kerekített lesz. Ha tehetjük (és most tehetjük), érdemesebb másik számítási módot keresni. Tudjuk, hogy a későbbiekben a szög szinuszára lesz szükségünk, ez pedig kiszámítható a szög koszinuszából; emeljük négyzetre:
196/260 = cos²α, és most jön a trükk; adjink hozzá sin²α-t:
196/260 +sin²α = cos²α + sin²α, így a tanultak alapján a jobb oldali kifejezés értéke pont 1:
196/260 +sin²α = 1, kivonás előtt egyszerűsítsük a törtet:
49/65 + sin²α = 1, kivonunk:
sin²α = 16/65, gyököt vonunk:
`sinα = 4/(√65)`
Itt elméletileg bejönne a sinα = -4/(√65)) megoldás is, gyakorlatilag pedig tudjuk, hogy az α szög 0° és 180° közé esik, ezekről pedig tudjuk, hogy mindegyik szinusza pozitív.
Innentől már csak a szinusztos területképletre van szükségünk:
`T = (|AB→|*|AC→|*sinα)/2 = (√(13)*√(20)*4/(√65))/2 = ... = 4`, tehát a háromszög területe 4 egység (ugyanezt a GeoGebra egy pillanat alatt kiszámolta, és az is 4-et adott, tehát biztosan jó a végeredmény).
Először számoljuk ki az oldalak vektorait (mindegy, hogy merre mutatnak, illetve majdnem teljesen, ezt később látni fogjuk, miért);
AB→=(-3;2)
AC→=(2;-4)
BC→=(5;-6), remélem, ezt nem kell külön ecsetelnem. Ha mégis kellene, szólj.
Most adott három vektor, ezeknek a hosszát ki tudjuk számolni a tanult módon (de ezt is részletezem, ha szükséges):
|AB→|=√ (-3)²+2² =√ 13
|AC→|=√ 2²+(-4)² =√ 20
|BC→|=√ 5²+(-6)² =√ 61
Mindenképp szükségünk van a háromszög egyik szögére, innen két lehetőség van;
1) Skaláris szorzattal;
Válasszuk ki valamelyik szöget, amelyre fel akarjuk írni a skaláris szorzatot. És itt lényeges az, hogy a fenti vektorokat hogyan írtuk fel; nekünk olyan vektorok kellenek, amelyek a háromszög ugyanazon csúcsából indulnak, és, persze, a háromszög oldalára esnek. Ennek csak az AB→ és AC→ vektorok felelnek meg (természetesen ki lehet számolni a BA→, CA→ és CB→ vektorokat is, így akármelyik szöget választhatjuk), így válasszuk ezeket a vektorokat; ha a vektorok hajlásszöge α, akkor a skaláris szorzat:
(AB→)*(AC→) = |AB→|*|AC→|*cosα
A bal oldali szorzat így fog alakulni: (-3;2)*(2;-4)=(-3)*2+2*(-4)=-14
A jobb oldalon csak be kell helyettesíteni, így:
-14 = √ 13 * √ 20 * cosα, rendezés után ezt kapjuk:
`-14/(√(260)) = cosα`
Egyelőre hagyjuk így ezt az egyenletet, 2)-ben úgyis visszaköszön, majd ott folytatjuk.
2) Koszinusztétellel;
Azt már korábban megtanultuk, hogy ha egy háromszög minden oldala ismert, akkor felírható rá a koszinusztétel. Itt már nem lényeges a vektorok állása, csak a hosszuk kell, így a már tanult módon felírjuk; legyen szintén az A csúcsnál lévő α szög a kitüntetett, ekkor:
|BC→|² = |AB→|² + |AC→|² - 2*|AB→|*|AC→|*cosα
Behylettesítés után:
√ 61 ² = √ 13 ²+√ 20 ² - 2*√ 13 *√ 20 *cosα
Rendezés után a fenti egyenletet kapjuk, vagyis:
`-14/(√(260)) = cosα`
Itt szintén két lehetőség van; az egyik, hogy kiszámoljuk az α szög nagyságát, és azzal számolunk tovább. Ezzel csak annyi a probléma, hogy mindenképp egy kerekített értékkel kellene továbbszámolnunk, így az eredmény is csak kerekített lesz. Ha tehetjük (és most tehetjük), érdemesebb másik számítási módot keresni. Tudjuk, hogy a későbbiekben a szög szinuszára lesz szükségünk, ez pedig kiszámítható a szög koszinuszából; emeljük négyzetre:
196/260 = cos²α, és most jön a trükk; adjink hozzá sin²α-t:
196/260 +sin²α = cos²α + sin²α, így a tanultak alapján a jobb oldali kifejezés értéke pont 1:
196/260 +sin²α = 1, kivonás előtt egyszerűsítsük a törtet:
49/65 + sin²α = 1, kivonunk:
sin²α = 16/65, gyököt vonunk:
`sinα = 4/(√65)`
Itt elméletileg bejönne a sinα = -4/(√65)) megoldás is, gyakorlatilag pedig tudjuk, hogy az α szög 0° és 180° közé esik, ezekről pedig tudjuk, hogy mindegyik szinusza pozitív.
Innentől már csak a szinusztos területképletre van szükségünk:
`T = (|AB→|*|AC→|*sinα)/2 = (√(13)*√(20)*4/(√65))/2 = ... = 4`, tehát a háromszög területe 4 egység (ugyanezt a GeoGebra egy pillanat alatt kiszámolta, és az is 4-et adott, tehát biztosan jó a végeredmény).
Módosítva: 7 éve
1
- Még nem érkezett komment!
 DomahidiPéter
válasza
DomahidiPéter
válasza
Itt egy egyszerübb megoldás!
Legyen egy ilyen háromszögünk
A={0,0)
B=(x,y)
C=(x",y")
Ekkor
T=|xy"-y×x"|/2
Mivel a mi esetünkben az A={2,3} ezért toljuk el a háromszöget egy
(-2,-3) as vektorral...
A(2,3) +(-2,-3)= A"(0,0)
B(-1,5). +(-2,-3)=B"(-3,2)
C(4,-1). +(-2,-3)=C"(2,-4)
T(ABC)=T(A"B"C")
Ezért alkalmazhatjuk a szabályt!
A"={0,0}
B"={-3,2}
C"={2,-4}
T={ (-3)×(-4)-2×2 }/2={12-4}/2=4
Ez könnyebb így számolni..
Legyen egy ilyen háromszögünk
A={0,0)
B=(x,y)
C=(x",y")
Ekkor
T=|xy"-y×x"|/2
Mivel a mi esetünkben az A={2,3} ezért toljuk el a háromszöget egy
(-2,-3) as vektorral...
A(2,3) +(-2,-3)= A"(0,0)
B(-1,5). +(-2,-3)=B"(-3,2)
C(4,-1). +(-2,-3)=C"(2,-4)
T(ABC)=T(A"B"C")
Ezért alkalmazhatjuk a szabályt!
A"={0,0}
B"={-3,2}
C"={2,-4}
T={ (-3)×(-4)-2×2 }/2={12-4}/2=4
Ez könnyebb így számolni..
Módosítva: 7 éve
1
- Még nem érkezett komment!