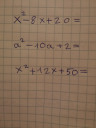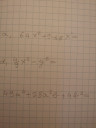Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Kérlek segítsetek megoldani ezeket! Szorzattá alakítás módszerei, azon belül kiemeléssel és keplettel
 Hikaru
kérdése
Hikaru
kérdése
957
Nagyon fontos lenne ezeknek a megoldása, ezen múlik a félévi jegyem
Valaki el tudná magyarázni is?
Előre is köszönöm aki meg tudja oldani, és segít!
Valaki el tudná magyarázni is?
Előre is köszönöm aki meg tudja oldani, és segít!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
3 bongolo
{
bongolo
{  }
válasza
}
válasza
Ezeket majdnem mind "teljes négyzetté alakítás" után lehet szorzattá alakítani.
A teljes négyzetté alakítás ezt jelenti:
Ismered azt a nevezetes képletet , hogy `(a+b)^2=a^2+2ab+b^2`
Ennek az elejéhez (`a^2+2·a·b`) hasonlót kell keresni!
(Az "eleje" alatt a négyzetes és az elsőfokú tagot értem.)
Majd a példával mutatom, hogyan kell továbmenni.
----
Első feladat:
`x^2-8x+20`
Ennek az "eleje" (vagyis a másod és elsőfokú tag) az `x^2-8x`, ami picit átírva `x^2-2·x·4`. Látod, hogy hasonlít a fenti elejéhez?
Ami fent `a`, az itt `x`
Ami fent `b`, az itt `-4`
Rá kell jönni így, hogy `(x-4)^2` eleje ugyanaz, mint a mi kifejezésünk eleje.
`(x-4)^2=x^2-2·4x+4^2=x^2-8x+16`
Ha ehhez még 4-et hozzáadunk, pontosan ugyanazt kapjuk:
`(x-4)^2+4=x^2-8x+20`
Ennyi volt a teljes négyzetté alakítás. Az jött tehát ki, hogy `(x-4)^2+4`
Hogyan lehet ebből szorzatot csinálni? Akkor lehetne, ha nem `+4` lenne a végén, hanem mínusz valamennyi. Ezt az elsőt nem lehet szorzattá alakítani.
----
Második:
`a^2-10a+2=a^2-2·5·a+2`
Ennek az eleje olyan, mint az `(a-5)^2` eleje:
`(a-5)^2=a^2-10a+25` (tiszta ugye?)
Ha ebből levonunk 23-at, pont ugyanazt kapjuk, mint ami a feladat:
`(a-5)^2-23=a^2-10a+25-23=a^2-10a+2`
Vagyis a teljes négyzet az `(a-5)^2-23`
Ebben mínusz van a végén, ezt lehet szorzattá alakítani! Mutatom, hogy:
Van az a nevezetes szorzat, hogy
`(x+y)(x-y)=x^2-y^2`
Ezt fogjuk visszafelé használni: ha van ket négyzetes kifejezés különbsége, abból tudunk szorzatot csinálni (ami a bal oldal).
Most az van, hogy `(a-5)^2-23`, amiben van egy darab négyzetes kifejezés, de pontosan kettő kellene. Könnyű csinálni:
`(a-5)^2-sqrt(23)^2`
amiből ez a szorzat lesz:
`((a-5)+sqrt(23))((a-5)-sqrt(23))`
`=(a-5+sqrt(23))(a-5-sqrt(23))`
------
Harmadik:
Próbáld magadtól teljes négyzetté alakítani. Nem mínusz valamennyi lesz, hanem plusz 14, ezért nem lehet szorzattá alakítani.
A teljes négyzetté alakítás ezt jelenti:
Ismered azt a nevezetes képletet , hogy `(a+b)^2=a^2+2ab+b^2`
Ennek az elejéhez (`a^2+2·a·b`) hasonlót kell keresni!
(Az "eleje" alatt a négyzetes és az elsőfokú tagot értem.)
Majd a példával mutatom, hogyan kell továbmenni.
----
Első feladat:
`x^2-8x+20`
Ennek az "eleje" (vagyis a másod és elsőfokú tag) az `x^2-8x`, ami picit átírva `x^2-2·x·4`. Látod, hogy hasonlít a fenti elejéhez?
Ami fent `a`, az itt `x`
Ami fent `b`, az itt `-4`
Rá kell jönni így, hogy `(x-4)^2` eleje ugyanaz, mint a mi kifejezésünk eleje.
`(x-4)^2=x^2-2·4x+4^2=x^2-8x+16`
Ha ehhez még 4-et hozzáadunk, pontosan ugyanazt kapjuk:
`(x-4)^2+4=x^2-8x+20`
Ennyi volt a teljes négyzetté alakítás. Az jött tehát ki, hogy `(x-4)^2+4`
Hogyan lehet ebből szorzatot csinálni? Akkor lehetne, ha nem `+4` lenne a végén, hanem mínusz valamennyi. Ezt az elsőt nem lehet szorzattá alakítani.
----
Második:
`a^2-10a+2=a^2-2·5·a+2`
Ennek az eleje olyan, mint az `(a-5)^2` eleje:
`(a-5)^2=a^2-10a+25` (tiszta ugye?)
Ha ebből levonunk 23-at, pont ugyanazt kapjuk, mint ami a feladat:
`(a-5)^2-23=a^2-10a+25-23=a^2-10a+2`
Vagyis a teljes négyzet az `(a-5)^2-23`
Ebben mínusz van a végén, ezt lehet szorzattá alakítani! Mutatom, hogy:
Van az a nevezetes szorzat, hogy
`(x+y)(x-y)=x^2-y^2`
Ezt fogjuk visszafelé használni: ha van ket négyzetes kifejezés különbsége, abból tudunk szorzatot csinálni (ami a bal oldal).
Most az van, hogy `(a-5)^2-23`, amiben van egy darab négyzetes kifejezés, de pontosan kettő kellene. Könnyű csinálni:
`(a-5)^2-sqrt(23)^2`
amiből ez a szorzat lesz:
`((a-5)+sqrt(23))((a-5)-sqrt(23))`
`=(a-5+sqrt(23))(a-5-sqrt(23))`
------
Harmadik:
Próbáld magadtól teljes négyzetté alakítani. Nem mínusz valamennyi lesz, hanem plusz 14, ezért nem lehet szorzattá alakítani.
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
megoldása
}
megoldása
Másik lap
a)
`64x^2+9-48x`
Először "rendes" sorrendbe érdemes rakni, hogy elől legyen a négyzetes, utána az elsőfokú tag:
`=64x^2-48x+9`
Aztán a négyzetes tagból "igazi" négyzetet kell csinálni. Tudjuk, hogy 8·8=64:
`=(8x)^2-48x+9`
Most már elől van egy "igazi" négyzet (`a^2`, ahol `a=8x`), utána a `2·a·b` jellegűnek kellene lennie. Alakítsuk olyanná:
`=(8x)^2-6·(8x)+9=(8x)^2-2·(8x)·3+9`
Ennek az eleje már teljesen olyan, mint az `a^2-2ab`, vagyis ez a teljes négyzetté alakítás:
`(8x-3)^2`
Ennek az eleje pont olyan, mint a miénk. Mennyi is ez?
`(8x-3)^2=(8x)^2-2·3·8x+3^2`
Hoppá, ez pontosan ugyanaz, mint ami ki kell nekünk jöjjön, nem is kell tovább menni, a teljes négyzetté alakítás szorzatot (négyzetet) csinált.
------
d)
`4/9x^2-y^2`
Ez most nem teljes négyzetté alakítás lesz, mert csak másodfokú tagok vannak benne (nincs elsőfokú), ezért nem tud `a^2+2ab` alakú lenni az "eleje".
Viszont pontosan két darab négyzetes tagból áll! Ha kicsit átalakítjuk, még jobban látszik:
`=(2/3)^2x^2-y^2=(2/3x)^2-y^2`
Ezt pedig már tudjuk, hogy szorzattá lehet alakítani: tudod, `a^2-b^2=(a+b)(a-b)`:
`=(2/3x+y)(2/3x-y)`
---
Utolsó:
`49a^4+28a^2b+4b^2`
Négyzeteket érdemes csinálni most is:
`=(7a^2)^2+28a^2b+(2b)^2`
Ha már van `7a^2` meg `2b` is, amiknek a négyzetét vettük, érdemes a köæépső tagban is ilyen kifejezéseket zárójelezni:
`=(7a^2)^2+2·(7a^2)(2b)+(2b)^2`
Most pedig teljes négyzetté alakítás jöhet: az elején van valaminek (`7a^2`) a négyzete, utána meg kétszer az a valami és még szorozva másvalamivel (`2b`), ezért ehhez a négyzethez hasonlít:
`((7a^2)+(2b))^2`
Szorozzuk vissza, hogy ez mennyi, és hoppá, pontosan a keresett kifejezés jön ki. Tehát ez a szorzat (négyzet):
`(7a^2+2b)^2`
a)
`64x^2+9-48x`
Először "rendes" sorrendbe érdemes rakni, hogy elől legyen a négyzetes, utána az elsőfokú tag:
`=64x^2-48x+9`
Aztán a négyzetes tagból "igazi" négyzetet kell csinálni. Tudjuk, hogy 8·8=64:
`=(8x)^2-48x+9`
Most már elől van egy "igazi" négyzet (`a^2`, ahol `a=8x`), utána a `2·a·b` jellegűnek kellene lennie. Alakítsuk olyanná:
`=(8x)^2-6·(8x)+9=(8x)^2-2·(8x)·3+9`
Ennek az eleje már teljesen olyan, mint az `a^2-2ab`, vagyis ez a teljes négyzetté alakítás:
`(8x-3)^2`
Ennek az eleje pont olyan, mint a miénk. Mennyi is ez?
`(8x-3)^2=(8x)^2-2·3·8x+3^2`
Hoppá, ez pontosan ugyanaz, mint ami ki kell nekünk jöjjön, nem is kell tovább menni, a teljes négyzetté alakítás szorzatot (négyzetet) csinált.
------
d)
`4/9x^2-y^2`
Ez most nem teljes négyzetté alakítás lesz, mert csak másodfokú tagok vannak benne (nincs elsőfokú), ezért nem tud `a^2+2ab` alakú lenni az "eleje".
Viszont pontosan két darab négyzetes tagból áll! Ha kicsit átalakítjuk, még jobban látszik:
`=(2/3)^2x^2-y^2=(2/3x)^2-y^2`
Ezt pedig már tudjuk, hogy szorzattá lehet alakítani: tudod, `a^2-b^2=(a+b)(a-b)`:
`=(2/3x+y)(2/3x-y)`
---
Utolsó:
`49a^4+28a^2b+4b^2`
Négyzeteket érdemes csinálni most is:
`=(7a^2)^2+28a^2b+(2b)^2`
Ha már van `7a^2` meg `2b` is, amiknek a négyzetét vettük, érdemes a köæépső tagban is ilyen kifejezéseket zárójelezni:
`=(7a^2)^2+2·(7a^2)(2b)+(2b)^2`
Most pedig teljes négyzetté alakítás jöhet: az elején van valaminek (`7a^2`) a négyzete, utána meg kétszer az a valami és még szorozva másvalamivel (`2b`), ezért ehhez a négyzethez hasonlít:
`((7a^2)+(2b))^2`
Szorozzuk vissza, hogy ez mennyi, és hoppá, pontosan a keresett kifejezés jön ki. Tehát ez a szorzat (négyzet):
`(7a^2+2b)^2`
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
0
-
Hikaru : Szia nem értem 7 éve 0
-
Hikaru : Le tudnád írni a megoldásait? 7 éve 0
-
bongolo: Nem. 7 éve 0
-
bongolo: (Ugyanis fentebb már leírtam, de nem vetted a fáradságot, hogy végigolvasd) 7 éve 0