Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
S.O.S csonkakúp
meixner_beatrix07
kérdése
926
Egy egyenes csonkakúp alapkörének sugara 33.42 cm , magassága 21.16 cm , alkotója 30.17 cm.
Mekkora a fedőlap sugara , és mekkora szöget zárnak be az alkotók az alaplappal?
Mekkora a fedőlap sugara , és mekkora szöget zárnak be az alkotók az alaplappal?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1
kazah
megoldása
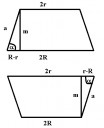
Ábra.
R=33.42 cm
m=21.16 cm
a=30.17 cm
Ott a derékszögű háromszög:
`(R-r)^2` + `m^2` = `a^2`
`(33.42-r)^2`+ `21.16^2` = `30.17^2`
|33.42-r| = 21.5
vagy
`r^2` - 66.84r + 654.4131 = 0
`r_1`= 54.92 cm
`r_2` = 11.92 cm
Nem találtam semmi olyan definíciót, ahol külön említenék, hogy az alaplap a nagyobb, lehet ez egy vödör is vagy egy virágcserép, szóval ha rosszul gondolom, elnézést, akkor csak az egyik megoldás kell (a kisebb), de várom a definíciókat. Olyat viszont találtam, hogy `-`a csonkakúp alaplapjai R és r `-`, szóval reménykedem, hogy mindkettő jó.
Itt már mindent ismerünk, akármelyik szögfüggvényt használhatjuk. (célszerű a megadott adatokat, akkor egyrészt nem görgetjük tovább a pontatlanság hibáját, másrészt ha elszámoltuk, nem visszük tovább az elszámolt eredményt.)
`sin alpha` = `m/a`= `21.16/30.17`
`alpha` = 44.54°
Ha a kisebbet tekintjük alaplapnak, akkor 180-44.54=135.46°
R=33.42 cm
m=21.16 cm
a=30.17 cm
Ott a derékszögű háromszög:
`(R-r)^2` + `m^2` = `a^2`
`(33.42-r)^2`+ `21.16^2` = `30.17^2`
|33.42-r| = 21.5
vagy
`r^2` - 66.84r + 654.4131 = 0
`r_1`= 54.92 cm
`r_2` = 11.92 cm
Nem találtam semmi olyan definíciót, ahol külön említenék, hogy az alaplap a nagyobb, lehet ez egy vödör is vagy egy virágcserép, szóval ha rosszul gondolom, elnézést, akkor csak az egyik megoldás kell (a kisebb), de várom a definíciókat. Olyat viszont találtam, hogy `-`a csonkakúp alaplapjai R és r `-`, szóval reménykedem, hogy mindkettő jó.
Itt már mindent ismerünk, akármelyik szögfüggvényt használhatjuk. (célszerű a megadott adatokat, akkor egyrészt nem görgetjük tovább a pontatlanság hibáját, másrészt ha elszámoltuk, nem visszük tovább az elszámolt eredményt.)
`sin alpha` = `m/a`= `21.16/30.17`
`alpha` = 44.54°
Ha a kisebbet tekintjük alaplapnak, akkor 180-44.54=135.46°
0
- Még nem érkezett komment!