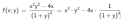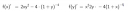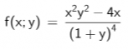Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Kétváltozós függvény parciális deriválása
 boros-mate5495
kérdése
boros-mate5495
kérdése
721
Sziasztok!
Ellenőrizni szeretném magam, hogy jól deriváltam. A képen csatoltam a függvényt, és a megoldásom.
Ellenőrizni szeretném magam, hogy jól deriváltam. A képen csatoltam a függvényt, és a megoldásom.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
3 bongolo
{
bongolo
{  }
válasza
}
válasza
Nem jó.
Eleve az első képen hogyan jött az, hogy a számlálót "csak úgy" leírod előre zárójel nélkül, aztán az utolsó tagját beszorzod a nevezővel (1 per nevezővel)??
Aztán f(x)' meg f(y)' jelölés mi akar lenni? Így nem szoktuk jelölni a parciális derváltat, az biztos.
Meg akkor általános iskolás vagy, mint ahogy az adatlapod mondja, vagy egyetemista?
Eleve az első képen hogyan jött az, hogy a számlálót "csak úgy" leírod előre zárójel nélkül, aztán az utolsó tagját beszorzod a nevezővel (1 per nevezővel)??
Aztán f(x)' meg f(y)' jelölés mi akar lenni? Így nem szoktuk jelölni a parciális derváltat, az biztos.
Meg akkor általános iskolás vagy, mint ahogy az adatlapod mondja, vagy egyetemista?
Módosítva: 7 éve
0
-
boros-mate5495: Egyetemista vagyok. Igen tudom nem így jelölik, de nem tudtam másképp beírni. 7 éve 0
-
boros-mate5495: Az adatlapom pedig módosítottam, bár nem tudom mi köze a kérdéshez
 7 éve
0
7 éve
0
 boros-mate5495
válasza
boros-mate5495
válasza
Ennek a függvénynek szeretném megtudni, a parciális deriváltjait x,y szerint, és a vegyes deriváltakat.
Módosítva: 7 éve
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
`f(x,y)=(x^2y^2-4x)/(1+y)^4`
A parciális deriváltat lehet jelölni mondjuk `f_x^'(x,y)` módon is, de én jobb szeretem úgy, hogy `(∂f)/(∂x)`
Egy `f/g` törtet úgy deriválunk, hogy `(f'·g-f·g')/g^2`. Parciális deriválás esetén is ugyanez a szabály.
Most a nevezőben nincs `x`, ezért `x` szerinti deriváláskor lehet úgy is tekinteni, mintha a nevezőben egy konstans lenne, szóval csak a számlálót kell deriválni.
`(∂f)/(∂x) = (2xy^2-4)/(1+y)^4`
(Ha végigcsinálod a törtes módon, abból is ugyanez jön ki persze.)
`y` szerint már muszáj a törtes szabályt használni:
`(∂f)/(∂y) = (2x^2y(1+y)^4-(x^2y^2-4x)·4(1+y)^3)/(1+y)^8=(2x^2y)/(1+y)^4-4(x^2y^2-4x)/(1+y)^5`
EDIT: fenti derivált javítva.
Ha kell vegyes deriváltat is csinálni, akkor nem kell esetleg ezt mindet?:
`(∂^2f)/(∂x^2), (∂^2f)/(∂y^2), (∂^2f)/(∂x∂y), (∂^2f)/(∂y∂x)`
Próbáld meg őket. Írd meg, mi lett, leellenőrzöm.
A parciális deriváltat lehet jelölni mondjuk `f_x^'(x,y)` módon is, de én jobb szeretem úgy, hogy `(∂f)/(∂x)`
Egy `f/g` törtet úgy deriválunk, hogy `(f'·g-f·g')/g^2`. Parciális deriválás esetén is ugyanez a szabály.
Most a nevezőben nincs `x`, ezért `x` szerinti deriváláskor lehet úgy is tekinteni, mintha a nevezőben egy konstans lenne, szóval csak a számlálót kell deriválni.
`(∂f)/(∂x) = (2xy^2-4)/(1+y)^4`
(Ha végigcsinálod a törtes módon, abból is ugyanez jön ki persze.)
`y` szerint már muszáj a törtes szabályt használni:
`(∂f)/(∂y) = (2x^2y(1+y)^4-(x^2y^2-4x)·4(1+y)^3)/(1+y)^8=(2x^2y)/(1+y)^4-4(x^2y^2-4x)/(1+y)^5`
EDIT: fenti derivált javítva.
Ha kell vegyes deriváltat is csinálni, akkor nem kell esetleg ezt mindet?:
`(∂^2f)/(∂x^2), (∂^2f)/(∂y^2), (∂^2f)/(∂x∂y), (∂^2f)/(∂y∂x)`
Próbáld meg őket. Írd meg, mi lett, leellenőrzöm.
Módosítva: 7 éve
0
-
boros-mate5495: Ha y szerint deriválom akkor a f' az nem az lesz, hogy x^2*2y ? Az x^2 lesz olyan mintha konstans lenne. 7 éve 0
-
boros-mate5495: Egyébként, hogy csinálod hogy ilyen szépen írod az egyenleteket? Valami programmal? 7 éve 0
-
bongolo: De, az lesz, copy-paste-teltem
 Javítom
7 éve
0
Javítom
7 éve
0
-
bongolo: ASCIIMath kódokat lehet írni. Lásd http://www.wjagray.co.uk/maths/ASCIIMathTutorial.html 7 éve 0
-
bongolo: (Magyar billentyűzeten AltGr-7 adja a backtick nevű `\`` karaktert 7 éve 0
-
bongolo: Hmm, most Chrome-ban nem jó a Tutorial valamiért... FireFox-ban jó. 7 éve 0