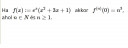Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Függvény deriválás
 gyula205
kérdése
gyula205
kérdése
443
A feladatot lásd az alábbi csatolmányban:
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
3 kazah
válasza
kazah
válasza
f(x)'=`e^x(x^2+3x+1)` + `e^x(2x+3)`
`e^0` = 1 és az x-es tagok 0-k az x=0 helyen.
f(0)'= `e^x˙*((x^2+ (3+2)*x + (3+1))`= 4
f(0)'' = `e^x(x^2 + (3+2+2)*x + (3+2+3+1))`= 9
.
.
.
`f(0)^((n))`= `e^x(x^2+ (3+2n)*x + 1+sum_1^n(2*n+1))` = `(n+1)^2`
`sum_1^a(1+2(a-1))` = `a^2`
a=n+1
1+ `sum(1+2n)` = `(n+1)^2`
Nekem `(n+1)^2` jött ki, de lehet, hogy én tévedek.
`e^0` = 1 és az x-es tagok 0-k az x=0 helyen.
f(0)'= `e^x˙*((x^2+ (3+2)*x + (3+1))`= 4
f(0)'' = `e^x(x^2 + (3+2+2)*x + (3+2+3+1))`= 9
.
.
.
`f(0)^((n))`= `e^x(x^2+ (3+2n)*x + 1+sum_1^n(2*n+1))` = `(n+1)^2`
`sum_1^a(1+2(a-1))` = `a^2`
a=n+1
1+ `sum(1+2n)` = `(n+1)^2`
Nekem `(n+1)^2` jött ki, de lehet, hogy én tévedek.
Módosítva: 7 éve
0
-
bongolo: Nem tévedsz, annyi az. 7 éve 0
 bongolo
{
bongolo
{  }
válasza
}
válasza
Jó kazah válasza, csak picit másképp csinálom:
Néhány deriválás után jön az ötlet, hogy teljes indukcióval bizonyára belátható ez:
`f^((n))(x)=e^x(x^2+(2n+3)x+(n+1)^2)`
`n`=0-ra igaz (az az eredeti fűggvény)
`n+1`-re pedig:
`f^((n+1))(x)=e^x(x^2+(2n+3)x+(n+1)^2)+e^x(2x+(2n+3))=`
`=e^x(x^2+(2+2n+3)x+(n+1)^2+2n+3)=`
`=e^x(x^2+(2(n+1)+3)x+((n+1)+1)^2)`
Tehát tényleg igaz.
Ezek után:
`f^((n))(0)=e^0(0^2+(2n+3)0+(n+1)^2)=(n+1)^2`
Nem `n^3` jön ki...
Néhány deriválás után jön az ötlet, hogy teljes indukcióval bizonyára belátható ez:
`f^((n))(x)=e^x(x^2+(2n+3)x+(n+1)^2)`
`n`=0-ra igaz (az az eredeti fűggvény)
`n+1`-re pedig:
`f^((n+1))(x)=e^x(x^2+(2n+3)x+(n+1)^2)+e^x(2x+(2n+3))=`
`=e^x(x^2+(2+2n+3)x+(n+1)^2+2n+3)=`
`=e^x(x^2+(2(n+1)+3)x+((n+1)+1)^2)`
Tehát tényleg igaz.
Ezek után:
`f^((n))(0)=e^0(0^2+(2n+3)0+(n+1)^2)=(n+1)^2`
Nem `n^3` jön ki...
0
-
gyula205: Teljesen igazatok van. A feladvány f(x):=x(x^2+3x+1) függvényhez kapcsolódik. Én néztem el a feladványösszeállításakor. És akkor már kijön valami. 7 éve 0
-
gyula205: Nem, nem! Teljesen szórakozott vagyok, mert inkább az f(x):=exp(x)x(x^2+3x+1) függvényről van szó. Dupla elnézést kérnék a kollégáktól! 7 éve 0
 bongolo
{
bongolo
{  }
megoldása
}
megoldása
Szóval `f(x) = e^x·x(x^2+3x+1)=e^x(x^3+3x^2+x)`
Az első néhány derivált ez:
`f'(x)=e^x(x^3+6x^2+7x+1)`
`f''(x)=e^x(x^3+9x^2+19x+8)`
`f^((3))(x)=e^x(x^3+12x^2+37x+27)`
Ebből annyi sejthető, hogy
`f^((n))(x)=e^x(x^3+3(n+1)x^2+"valami"·x+n^3)`
Ez persze csak sejtés, ráadásul a lineáris tag együtthatója nem ismerős...
Ha viszont ezt deriváljuk, ez lesz:
`f^((n+1))(x)=e^x(x^3+3(n+2)x^2+("valami"+6(n+1))·x+n^3+"valami")`
A lineáris tag együtthatója tehát egy ilyen sorozat:
`a(0)=1`
`a(n)=a(n-1)+6n`
vagy ha ezt kibontjuk (illetve lehet, hogy könnyebben látszik, ha az első deriválttól kezdve nézzük, hogy mik adódtak össze) :
`a(n)=1+sum_(k=1)^n 6k=1+6·(n·(n+1))/2`
hisz a legegyszerűbb számtani sorozat összegének a 6-szorosa van az 1-hez adva.
`a(n)=3n^2+3n+1`
Tehát a sejtésünk ez:
`f^((n))(x)=e^x(x^3+3(n+1)x^2+(3n^2+3n+1)·x+n^3)`
Ezt megint teljes indukcióval bizonyíthatjuk:
`n=1`-re teljesül.
Feltesszük, hogy `n`-re igaz, nézzük meg `n+1`-re:
`f^((n+1))(x)=d/(dx) f^((n))(x)=`
`=e^x(x^3+3(n+2)x^2+((3n^2+3n+1)+6(n+1))·x+n^3+(3n^2+3n+1))`
`=e^x(x^3+3(n+2)x^2+((3n^2+6n+3)+(3n+3)+1)·x+(n^3+3n^2+3n+1))`
`=e^x(x^3+3(n+2)x^2+(3(n+1)^2+3(n+1)+1)·x+(n+1)^3)`
Tehát beláttuk, hogy `n+1`-re is a sejtett alakú összefüggés jön ki.
Vagyis bizonyítottuk,. hogy
`f^((n))(x)=e^x(x^3+3(n+1)x^2+(3n^2+3n+1)·x+n^3)`
Akkor pedig
`f^((n))(0)=e^0·(0^3+3(n+1)0^2+(3n^2+3n+1)·0+n^3)=n^3`
Az első néhány derivált ez:
`f'(x)=e^x(x^3+6x^2+7x+1)`
`f''(x)=e^x(x^3+9x^2+19x+8)`
`f^((3))(x)=e^x(x^3+12x^2+37x+27)`
Ebből annyi sejthető, hogy
`f^((n))(x)=e^x(x^3+3(n+1)x^2+"valami"·x+n^3)`
Ez persze csak sejtés, ráadásul a lineáris tag együtthatója nem ismerős...
Ha viszont ezt deriváljuk, ez lesz:
`f^((n+1))(x)=e^x(x^3+3(n+2)x^2+("valami"+6(n+1))·x+n^3+"valami")`
A lineáris tag együtthatója tehát egy ilyen sorozat:
`a(0)=1`
`a(n)=a(n-1)+6n`
vagy ha ezt kibontjuk (illetve lehet, hogy könnyebben látszik, ha az első deriválttól kezdve nézzük, hogy mik adódtak össze) :
`a(n)=1+sum_(k=1)^n 6k=1+6·(n·(n+1))/2`
hisz a legegyszerűbb számtani sorozat összegének a 6-szorosa van az 1-hez adva.
`a(n)=3n^2+3n+1`
Tehát a sejtésünk ez:
`f^((n))(x)=e^x(x^3+3(n+1)x^2+(3n^2+3n+1)·x+n^3)`
Ezt megint teljes indukcióval bizonyíthatjuk:
`n=1`-re teljesül.
Feltesszük, hogy `n`-re igaz, nézzük meg `n+1`-re:
`f^((n+1))(x)=d/(dx) f^((n))(x)=`
`=e^x(x^3+3(n+2)x^2+((3n^2+3n+1)+6(n+1))·x+n^3+(3n^2+3n+1))`
`=e^x(x^3+3(n+2)x^2+((3n^2+6n+3)+(3n+3)+1)·x+(n^3+3n^2+3n+1))`
`=e^x(x^3+3(n+2)x^2+(3(n+1)^2+3(n+1)+1)·x+(n+1)^3)`
Tehát beláttuk, hogy `n+1`-re is a sejtett alakú összefüggés jön ki.
Vagyis bizonyítottuk,. hogy
`f^((n))(x)=e^x(x^3+3(n+1)x^2+(3n^2+3n+1)·x+n^3)`
Akkor pedig
`f^((n))(0)=e^0·(0^3+3(n+1)0^2+(3n^2+3n+1)·0+n^3)=n^3`
0
- Még nem érkezett komment!