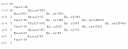Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Hermite interpoláció?
 gabor199808
kérdése
gabor199808
kérdése
504
Valaki megtudná ezt oldani és eltudná magyarázni, hogy kell és hogy hogyan is működik ez az interpoláció?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
3 bongolo
{
bongolo
{  }
válasza
}
válasza
A Newton interpolációt érdemes először megérteni. Abban nincsenek deriváltak, csak a függvényértékek.
Vagyis `(x_0, f(x_0)), (x_1, f(x_1)), (x_2, f(x_2))` stb szám-párokból indulunk ki.
Aztán ki kell számolni a differencia-hányados-szerű hányadosokat (osztott differenciáknak szokták hívni), vagyis ezeket:
`(f(x_1)-f(x_0))/(x_1-x_0), (f(x_2)-f(x_1))/(x_2-x_1)` stb.
Ezeket úgy szoktuk jelölni, hogy `f[x_1,x_0], f[x_2,x_1]` stb., az `f` után szögletes zárójelben van, hogy milyen `x`-ek osztott differenciájáról van szó.
Aztán ezeknek az osztott differenciáit is hasonlóan: pl. `f[x_1,x_0]` és `f[x_2,x_1]` hányadosa ez:
`f[x_2,x_1,x_0]=(f[x_2,x_1]-f[x_1,x_0])/(x_2-x_0)`
Mindezt ilyen háromszög-alakú ábrán szoktuk leírni:
`{:
(x_0,f(x_0), , , )
,( , , f[x_1,x_0], , )
,(x_1,f(x_1), , f[x_2,x_1,x_0] , )
,( , , f[x_2,x_1], , f[x_3,x_2,x_1,x_0])
,(x_2,f(x_2), , f[x_3,x_2,x_1] , )
,( , , f[x_3,x_2], , )
,(x_3,f(x_3), , , )
:}`
Ha sokat kellene írni, akkor mondjuk `f[x_3,x_2,x_1,x_0]` írható úgy is, hogy `f[x_3 ... x_0]` és ezt a hányadost jelenti:
`f[x_3 ... x_0]=(f[x_3 ... x_1]-f[x_2...x_0))/(x_3-x_0)`
Az interpolált polinom pedig ez lesz:
`f(x_0)+f[x_1,x_0]·(x-x_0)+f[x_2...x_0]·(x-x_1)(x-x_0)+f[x_3...x_0]·(x-x_2)(x-x_1)(x-x_0)`
Folytatom a Hermite-tel...
Vagyis `(x_0, f(x_0)), (x_1, f(x_1)), (x_2, f(x_2))` stb szám-párokból indulunk ki.
Aztán ki kell számolni a differencia-hányados-szerű hányadosokat (osztott differenciáknak szokták hívni), vagyis ezeket:
`(f(x_1)-f(x_0))/(x_1-x_0), (f(x_2)-f(x_1))/(x_2-x_1)` stb.
Ezeket úgy szoktuk jelölni, hogy `f[x_1,x_0], f[x_2,x_1]` stb., az `f` után szögletes zárójelben van, hogy milyen `x`-ek osztott differenciájáról van szó.
Aztán ezeknek az osztott differenciáit is hasonlóan: pl. `f[x_1,x_0]` és `f[x_2,x_1]` hányadosa ez:
`f[x_2,x_1,x_0]=(f[x_2,x_1]-f[x_1,x_0])/(x_2-x_0)`
Mindezt ilyen háromszög-alakú ábrán szoktuk leírni:
`{:
(x_0,f(x_0), , , )
,( , , f[x_1,x_0], , )
,(x_1,f(x_1), , f[x_2,x_1,x_0] , )
,( , , f[x_2,x_1], , f[x_3,x_2,x_1,x_0])
,(x_2,f(x_2), , f[x_3,x_2,x_1] , )
,( , , f[x_3,x_2], , )
,(x_3,f(x_3), , , )
:}`
Ha sokat kellene írni, akkor mondjuk `f[x_3,x_2,x_1,x_0]` írható úgy is, hogy `f[x_3 ... x_0]` és ezt a hányadost jelenti:
`f[x_3 ... x_0]=(f[x_3 ... x_1]-f[x_2...x_0))/(x_3-x_0)`
Az interpolált polinom pedig ez lesz:
`f(x_0)+f[x_1,x_0]·(x-x_0)+f[x_2...x_0]·(x-x_1)(x-x_0)+f[x_3...x_0]·(x-x_2)(x-x_1)(x-x_0)`
Folytatom a Hermite-tel...
Módosítva: 7 éve
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
megoldása
}
megoldása
A Hermite ettől abban különbözik, hogy felhasználja a függvény deriváltjait is, ha van olyan adat bizonyos x-eknél.
Mondjuk most ezek az x-ek vannak:
`x_0=-2, x_1=-1, x_2=1`
és `x_1`-hez van két derivált is, a többihez 1-1.
Mindegyik x-et megsokszorozzuk annyiszor, ahány derivált van hozzá:
`z_0="-2"`
`z_1="-2"` mert van első derivált
`z_2="-1"` (ez az `x_1`)
`z_3="-1"` mert van első derivált
`z_4="-1"` mert van második derivált
`z_5=1` (ez az `x_3`)
`z_6=1` mert van első derivált
És ezekkel csinálunk olyasmit, mint a Newton interpolációnál.
Viszont ilyenkor azok az osztott differenciák, amik azonos x-ekből származnak, azok 0/0 értékűek lennének, ami hülyeség. Ezeknél a hányados helyett a derivált szerepel, osztva n-faktoriálissal, ahol n az "emelet" száma. Az első derivált 1!-sal van osztva, a második derivált 2!-tal, stb.
Az adott esetben olyan táblázat lesz ebből, mint amit ez az ábra mutat (remélem, jól számoltam a hányadosokat, számolj utána)
Mondjuk most ezek az x-ek vannak:
`x_0=-2, x_1=-1, x_2=1`
és `x_1`-hez van két derivált is, a többihez 1-1.
Mindegyik x-et megsokszorozzuk annyiszor, ahány derivált van hozzá:
`z_0="-2"`
`z_1="-2"` mert van első derivált
`z_2="-1"` (ez az `x_1`)
`z_3="-1"` mert van első derivált
`z_4="-1"` mert van második derivált
`z_5=1` (ez az `x_3`)
`z_6=1` mert van első derivált
És ezekkel csinálunk olyasmit, mint a Newton interpolációnál.
Viszont ilyenkor azok az osztott differenciák, amik azonos x-ekből származnak, azok 0/0 értékűek lennének, ami hülyeség. Ezeknél a hányados helyett a derivált szerepel, osztva n-faktoriálissal, ahol n az "emelet" száma. Az első derivált 1!-sal van osztva, a második derivált 2!-tal, stb.
Az adott esetben olyan táblázat lesz ebből, mint amit ez az ábra mutat (remélem, jól számoltam a hányadosokat, számolj utána)
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
Tehát mondjuk a második osztott differenciák oszlopában a középső az derivált lesz: `(f''(z_2))/(2!)`, mert a tőle balra fent és lent lévő két számból kellene kiszámolni, de azok egyformák, ezért 0/0 lenne belőlük.
Aztán pl. az `f[z_5..z_2]` úgy jön ki, hogy a tőle balra fent és lent lévő két számnak kell venni a differenciáját `("-8"/2-"-16"/2=4)`, aztán osztani kell `z_5-z_2=1-(-1)` értékkel.
Számold végig mindet, lehet, hogy elrontottam valahol.
Miután megvan ez a háromszög, le lehet róla olvasni a polinomot a felső ferde vonalból (a tetejéből):
`"-10"+("-20")·(x-z_0)+28(x-z_1)(x-z_0)+("-26")(x-z_2)(x-z_1)(x-z_0)\ ...` stb.
Ilyesmi lesz:
`-10 -20(x+2) +28(x+2)² -26(x+1)(x+2)² +16(x+1)²(x+2)² -40/9 (x+1)³(x+2)² +35/27 (x-1)(x+1)³(x+2)²`
Ezt illene még kifejteni és összevonni, hogy rendes polinom-kinézetű legyen. Nem lesz szép, úgyhogy lehet, hogy elrontottam valahol a számolást.
Aztán pl. az `f[z_5..z_2]` úgy jön ki, hogy a tőle balra fent és lent lévő két számnak kell venni a differenciáját `("-8"/2-"-16"/2=4)`, aztán osztani kell `z_5-z_2=1-(-1)` értékkel.
Számold végig mindet, lehet, hogy elrontottam valahol.
Miután megvan ez a háromszög, le lehet róla olvasni a polinomot a felső ferde vonalból (a tetejéből):
`"-10"+("-20")·(x-z_0)+28(x-z_1)(x-z_0)+("-26")(x-z_2)(x-z_1)(x-z_0)\ ...` stb.
Ilyesmi lesz:
`-10 -20(x+2) +28(x+2)² -26(x+1)(x+2)² +16(x+1)²(x+2)² -40/9 (x+1)³(x+2)² +35/27 (x-1)(x+1)³(x+2)²`
Ezt illene még kifejteni és összevonni, hogy rendes polinom-kinézetű legyen. Nem lesz szép, úgyhogy lehet, hogy elrontottam valahol a számolást.
Módosítva: 7 éve
0
- Még nem érkezett komment!