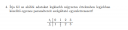Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Négyzetes közelítés 2
 gabor199808
kérdése
gabor199808
kérdése
531
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
Egyenes, tehát `f(t)=x_1 t+x_2` alakú függvénykapcsolatot keresünk. Helyettesítsük be a megadott adatokat:
`1=x_2`
`3/2=x_1+x_2`
`2=2x_1+x_2`
`3=3x_1+x_2`
És a feladat tulajdonképpen csak ennyit kért. De ha már itt vagyunk, oldjuk is meg. Most nincs olyan szerencsénk, mint az előző kérdésednél, ez az egyenletrendszer túlhatározott, egymásnak ellentmondó egyenleteket tartalmaz (vagyis a megadott adatpontok nem esnek egy egyenesre). Írjuk fel mátrixos alakban:
Most nincs olyan szerencsénk, mint az előző kérdésednél, ez az egyenletrendszer túlhatározott, egymásnak ellentmondó egyenleteket tartalmaz (vagyis a megadott adatpontok nem esnek egy egyenesre). Írjuk fel mátrixos alakban:
`[[1],[3/2],[2],[3]]=[[0,1],[1,1],[2,1],[3,1]] [[x_1],[x_2]]`
Ennek a legkisebb négyzetes értelemben optimális megoldása az alábbi vektor:
`[[x_1],[x_2]]^\text{*}``=``[[0,1],[1,1],[2,1],[3,1]]^+ *[[1],[3/2],[2],[3]]``=``[[-0.3,-0.1,0.1,0.3],[0.7,0.4,0.1,-0.2]]*[[1],[3/2],[2],[3]]``=``[[0.65],[0.9]]`
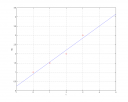
Itt a `+` jellel a mátrix Moore–Penrose-féle pszeudoinverzét jelöltem. Tehát a megoldás `f(t)=0.65 t+0.9`. Ezen most nincsenek pontosan rajta a megadott adatok, csak nagyjából (képet mellékeltem).
`1=x_2`
`3/2=x_1+x_2`
`2=2x_1+x_2`
`3=3x_1+x_2`
És a feladat tulajdonképpen csak ennyit kért. De ha már itt vagyunk, oldjuk is meg.
 Most nincs olyan szerencsénk, mint az előző kérdésednél, ez az egyenletrendszer túlhatározott, egymásnak ellentmondó egyenleteket tartalmaz (vagyis a megadott adatpontok nem esnek egy egyenesre). Írjuk fel mátrixos alakban:
Most nincs olyan szerencsénk, mint az előző kérdésednél, ez az egyenletrendszer túlhatározott, egymásnak ellentmondó egyenleteket tartalmaz (vagyis a megadott adatpontok nem esnek egy egyenesre). Írjuk fel mátrixos alakban:`[[1],[3/2],[2],[3]]=[[0,1],[1,1],[2,1],[3,1]] [[x_1],[x_2]]`
Ennek a legkisebb négyzetes értelemben optimális megoldása az alábbi vektor:
`[[x_1],[x_2]]^\text{*}``=``[[0,1],[1,1],[2,1],[3,1]]^+ *[[1],[3/2],[2],[3]]``=``[[-0.3,-0.1,0.1,0.3],[0.7,0.4,0.1,-0.2]]*[[1],[3/2],[2],[3]]``=``[[0.65],[0.9]]`
Itt a `+` jellel a mátrix Moore–Penrose-féle pszeudoinverzét jelöltem. Tehát a megoldás `f(t)=0.65 t+0.9`. Ezen most nincsenek pontosan rajta a megadott adatok, csak nagyjából (képet mellékeltem).
0
- Még nem érkezett komment!