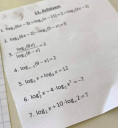Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Ligaritmikus egyenletek?
 norbinho01
kérdése
norbinho01
kérdése
495
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
5 kazah
válasza
kazah
válasza
1,
logaritmus azonosságok mennek?
Mindig első feladat, hogy felírjuk, mik a feltételek, mi nem lehet x.
A logaritmuson belül mindig >0
1. x>2
2. x>11
3. x>0.5
Tehát x>2 kell, hogy legyen.
`(6x-3)(x-11)`=`9(2x-1)`
`6x^2-87x+42=0`
`x_1`=`1/2`, `x_2`=14
A kezdeti feltételeknek a második gyök tesz eleget, így csak a x=14 gyöke az egyenletnek.
Ellenőrzés!
logaritmus azonosságok mennek?
Mindig első feladat, hogy felírjuk, mik a feltételek, mi nem lehet x.
A logaritmuson belül mindig >0
1. x>2
2. x>11
3. x>0.5
Tehát x>2 kell, hogy legyen.
`(6x-3)(x-11)`=`9(2x-1)`
`6x^2-87x+42=0`
`x_1`=`1/2`, `x_2`=14
A kezdeti feltételeknek a második gyök tesz eleget, így csak a x=14 gyöke az egyenletnek.
Ellenőrzés!
0
- Még nem érkezett komment!
 kazah
válasza
kazah
válasza
2.
Kezdeti feltételek:
1. x>`1/3`
2. `x<5`
tehát `1/3<x<5` kell, hogy teljesüljön.
`(6x-2)/(5-x)`=8
6x-2=8(5-x)
`x`= 3
Megfelel a feltételeknek, ez a gyöke az egyenletnek.
Ellenőrzés!
Kezdeti feltételek:
1. x>`1/3`
2. `x<5`
tehát `1/3<x<5` kell, hogy teljesüljön.
`(6x-2)/(5-x)`=8
6x-2=8(5-x)
`x`= 3
Megfelel a feltételeknek, ez a gyöke az egyenletnek.
Ellenőrzés!
0
- Még nem érkezett komment!
 kazah
megoldása
kazah
megoldása
3.Felt: x>0 és x<6
tehát: 0<x<6
szorozzuk a nevezővel és logaritmustalanítunk.
8x=`(6-x)^2`
`x^2-20x+36=0`
`x_1=18`, `x_2=2`
A kezdeti feltételeknek csak a második gyök felel meg.
Ellenőrzés!
tehát: 0<x<6
szorozzuk a nevezővel és logaritmustalanítunk.
8x=`(6-x)^2`
`x^2-20x+36=0`
`x_1=18`, `x_2=2`
A kezdeti feltételeknek csak a második gyök felel meg.
Ellenőrzés!
0
- Még nem érkezett komment!
 kazah
válasza
kazah
válasza
4.
feltételek: x<9
x>3, x<>4
`(x-3)^2=9-x`
x(x-5)=0
`x_1`=0, `x_2`=5
Csak a második gyök felel meg a feltételeknek.
Ellenőrzés!
5.
feltételek: x>0
`log_2 (x)=3*log_8 (x)`
`4*log_8 (x)=12`
`log_8 (x)=3
x=`8^3= 512
Ellenőrzés!
6.
feltételek: x>0
log_2 (x)=a
`a^2-8a+7`=0
(a-1)(a-7)=0
a,
`a_1`=1
log_2(x)=1 -> x=2
b,
`a_2`=7
log_2(x)=7 -> `x=2^7`=128
Mindkettő megfelel a feltételeknek, mindkettő megoldás.
Ellenőrzés!
7. feltételek: x>0, x<>1
Fogalmam sincs, feltételezzük, hogy 2 valamelyik hatványa lesz a megoldás, érdemes kipróbálni. 2 biztos nem, 4: az lesz a jó.
feltételek: x<9
x>3, x<>4
`(x-3)^2=9-x`
x(x-5)=0
`x_1`=0, `x_2`=5
Csak a második gyök felel meg a feltételeknek.
Ellenőrzés!
5.
feltételek: x>0
`log_2 (x)=3*log_8 (x)`
`4*log_8 (x)=12`
`log_8 (x)=3
x=`8^3= 512
Ellenőrzés!
6.
feltételek: x>0
log_2 (x)=a
`a^2-8a+7`=0
(a-1)(a-7)=0
a,
`a_1`=1
log_2(x)=1 -> x=2
b,
`a_2`=7
log_2(x)=7 -> `x=2^7`=128
Mindkettő megfelel a feltételeknek, mindkettő megoldás.
Ellenőrzés!
7. feltételek: x>0, x<>1
Fogalmam sincs, feltételezzük, hogy 2 valamelyik hatványa lesz a megoldás, érdemes kipróbálni. 2 biztos nem, 4: az lesz a jó.
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
7)
A logaritmusnál az egyik alapról (`a`) a másikra (`b`) így lehet áttérni:
`log_a(x)=log_b(x)/log_b(a)`
Most az `x` alapról érdemes 2-es alapra áttérni:
`log_x(2)=log_2(2)/log_2(x)=1/log_2(x)`
Innen már megy? Vezess be egy új változót, lesz egy másodfokú egyenlet, stb.
A logaritmusnál az egyik alapról (`a`) a másikra (`b`) így lehet áttérni:
`log_a(x)=log_b(x)/log_b(a)`
Most az `x` alapról érdemes 2-es alapra áttérni:
`log_x(2)=log_2(2)/log_2(x)=1/log_2(x)`
Innen már megy? Vezess be egy új változót, lesz egy másodfokú egyenlet, stb.
0
- Még nem érkezett komment!