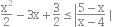Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Egyenlőtlenség
 borderless
{ Kérdező } kérdése
borderless
{ Kérdező } kérdése
690
Hány egész megoldása van a következő egyenlőtlenségnek?
2
4
5
6
2
4
5
6
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 zsofmoln
{ Tanár }
megoldása
zsofmoln
{ Tanár }
megoldása
4 szerintem. Az abszolútérték miatt. Ha ugyanis az abszolutértéken belül pozitív szám van az két megoldást von maga után (mert egy tört akkor pozitív ha a számláló és a nevező előjele megegyezik).
Pozitív számláló / pozitív nevező
Vagy
Negatív számláló / negatív nevező
Ha az abszolutérték negatív akkor is két megoldás lehetséges (mert egy tört akkor negatív előjelű ha vagy a számláló vagy a nevező negatív)
Pozitív számláló / negatív nevező
Vagy
Negatív számlálo/ pozitív nevező
Pozitív számláló / pozitív nevező
Vagy
Negatív számláló / negatív nevező
Ha az abszolutérték negatív akkor is két megoldás lehetséges (mert egy tört akkor negatív előjelű ha vagy a számláló vagy a nevező negatív)
Pozitív számláló / negatív nevező
Vagy
Negatív számlálo/ pozitív nevező
0
- Még nem érkezett komment!
 Rantnad
{
Rantnad
{  }
válasza
}
válasza
Első körben a jobb oldali törtből emeljünk ki -1-et:
=(-1)*(x-5)/(x-4), így a jobb oldalon ez lesz:
|(-1)*(x-5)/(x-4)|, tudjuk, hogy |a|*|b|=|a*b| (ez azért van, mert az || csak az előjelet változtatja, ami mindenképp pozitív lesz), ezért szétbonthatjuk így: |-1|*|(x-5)/(x-4)|, ez pedig így |(x-5)/(x-4)|-gyel egyenlő. Ezt a két törtet el tudjuk osztani egymással, ha egy kicsit átalakítjuk: x-5=x-4-1, tehát a törtből (x-4-1)/(x-4) lesz. Ez a törtekre vonatkozó összeadási szabály miatt szétbontható így: (x-4)/(x-4) -1/(x-4), ebből 1 - 1/(x-4) lesz. Nem nehéz rájönni, hogy 1/(x-4) értéke -1 és 1 között mozoghat; x=3 esetén -1, x=5 esetén 1, és mivel a nevező mindig lesz 1-nél, illetve kisebb lesz -1-nél, ezért a tört értéke csak -1 és 1 közé eshet. Emiatt az 1 -1/(x-4) értéke 2 és 0 között fog mozogni. Tehát ha a bal oldal értéke 2-nél nagyobb, akkor biztos, hogy nem lesz az egyenlőtlenségnek megoldása, ezért meg kell oldanunk ezt az egyenlőtlenséget:
x2 -3x +3/2 > 2, szorzunk 2-vel:
x2 -6x +3 > 4, kivonunk 4-et
x2 -6x -1 > 0, ezt úgy oldjuk meg, hogy a gyökök segítségével szorzatalakban felírjuk:
x1=(6+√ 40 )/2=~6,16, x2=(6-√ 40 )/2=~-0,162, tehát a bal oldal felírható így:
(x-6,16)*(x+0,162) > 0, ez akkor teljesül, ha a tényezők előjele azonos, tehát x>6,16 és x<-0,162 esetén lesz igaz, tehát ezek az x-ek kiesnek az eredeti egyenlőtlenség megoldáshalmazából. Ezek alapján marad 0,1,2,3,4,5,6, ebből a 4 kiesik, mivel akkor a jobb oldalon 0-val kellene osztani. A többit manuálisan be kell írogatni x helyére az eredeti egyenlőtlenségben:
x=0: 1,5 < 1,25, ez nem jó megoldás
x=1: -1 < 4/3, ez jó
x=2: -2,5 < 1,5, ez is jó
x=3: -3 < 2, ez is jó
x=5: -1 <0, ez is jó.
Tehát az egyenlőtlenségnek 4 megoldása van.
Az első válaszoló érvelése hibás, lévén, ha a számlálóban pl. nem 5-x lenne, hanem 100-x, máris több megoldás lenne (szám szerint 11, ebbe most nem mennék bele részletesebben).
=(-1)*(x-5)/(x-4), így a jobb oldalon ez lesz:
|(-1)*(x-5)/(x-4)|, tudjuk, hogy |a|*|b|=|a*b| (ez azért van, mert az || csak az előjelet változtatja, ami mindenképp pozitív lesz), ezért szétbonthatjuk így: |-1|*|(x-5)/(x-4)|, ez pedig így |(x-5)/(x-4)|-gyel egyenlő. Ezt a két törtet el tudjuk osztani egymással, ha egy kicsit átalakítjuk: x-5=x-4-1, tehát a törtből (x-4-1)/(x-4) lesz. Ez a törtekre vonatkozó összeadási szabály miatt szétbontható így: (x-4)/(x-4) -1/(x-4), ebből 1 - 1/(x-4) lesz. Nem nehéz rájönni, hogy 1/(x-4) értéke -1 és 1 között mozoghat; x=3 esetén -1, x=5 esetén 1, és mivel a nevező mindig lesz 1-nél, illetve kisebb lesz -1-nél, ezért a tört értéke csak -1 és 1 közé eshet. Emiatt az 1 -1/(x-4) értéke 2 és 0 között fog mozogni. Tehát ha a bal oldal értéke 2-nél nagyobb, akkor biztos, hogy nem lesz az egyenlőtlenségnek megoldása, ezért meg kell oldanunk ezt az egyenlőtlenséget:
x2 -3x +3/2 > 2, szorzunk 2-vel:
x2 -6x +3 > 4, kivonunk 4-et
x2 -6x -1 > 0, ezt úgy oldjuk meg, hogy a gyökök segítségével szorzatalakban felírjuk:
x1=(6+√ 40 )/2=~6,16, x2=(6-√ 40 )/2=~-0,162, tehát a bal oldal felírható így:
(x-6,16)*(x+0,162) > 0, ez akkor teljesül, ha a tényezők előjele azonos, tehát x>6,16 és x<-0,162 esetén lesz igaz, tehát ezek az x-ek kiesnek az eredeti egyenlőtlenség megoldáshalmazából. Ezek alapján marad 0,1,2,3,4,5,6, ebből a 4 kiesik, mivel akkor a jobb oldalon 0-val kellene osztani. A többit manuálisan be kell írogatni x helyére az eredeti egyenlőtlenségben:
x=0: 1,5 < 1,25, ez nem jó megoldás
x=1: -1 < 4/3, ez jó
x=2: -2,5 < 1,5, ez is jó
x=3: -3 < 2, ez is jó
x=5: -1 <0, ez is jó.
Tehát az egyenlőtlenségnek 4 megoldása van.
Az első válaszoló érvelése hibás, lévén, ha a számlálóban pl. nem 5-x lenne, hanem 100-x, máris több megoldás lenne (szám szerint 11, ebbe most nem mennék bele részletesebben).
1
- Még nem érkezett komment!