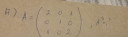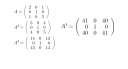Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek házi - mátrix
 Törölt
{ Kérdező } kérdése
Törölt
{ Kérdező } kérdése
821
Mátrix n-hatványra való emelése. Elkezdtem, de nem sikerült végig vinnem. :(
Jelenleg 1 felhasználó nézi ezt a kérdést.
Matek, mátrix
Matek, mátrix
0
Középiskola / Matematika
Válaszok
2 szzs
{ Fortélyos }
válasza
szzs
{ Fortélyos }
válasza
Melyik lépésnél van a gond?
Ezt is használhatod: https://www.geogebra.org/m/gmavHspE
Ezt is használhatod: https://www.geogebra.org/m/gmavHspE
Módosítva: 7 éve
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
megoldása
}
megoldása
Ami hatvány-eredményeket szzs írt, abból az a sejtés látszik, hogy az n-edik ilyesmi lesz:
`((f+1,0,f),(0,1,0),(f,0,f+1))`
Egyelőre ez csak sejtés, de n=1-re meg még további kis n-ekre is igaz. Teljes indukcióval be tudjuk látni, hogy minden n-re igaz. Ehhez elég annyi, hogy n=1-re igaz, feltesszük, hogy n-re is, aztán megnézzük n+1-re:
`((f+1,0,f),(0,1,0),(f,0,f+1))·((2,0,1),(0,1,0),(1,0,2))=(((f+1)·2+f,0,(f+1)+f·2),(0,1,0),(f·2+(f+1),0,f+(f+1)·2))`
`=((3f+2,0,3f+1),(0,1,0),(3f+1,0,3f+2))=((g+1,0,g),(0,1,0),(g,0,g+1))` ahol `g=3f+1`
Ez is tényleg olyan alakú mátrix, tehát teljes indukcióval beláttuk, hogy mindegyik hatvány ilyen alakú.
Ki kellene még találni, hogy mi `f` értéke az `n` függvényében. Láttuk, hogy `g=3f+1`, vagy máshogy írva: `f_(n+1)=3·f_n+1`
`f_1=1`
`f_2=3+1`
`f_3=3(3+1)+1=9+3+1`
`f_4=3(9+3+1)+1=27+9+3+1`
Szóval jó sok 3 hatványt kell összeadni.
Vagyis általánosan:
`f_n=sum_(k=0)^(n-1) 3^k`
ami egy mértani sorozat összege, ahol `a_1=1, q=3` és `n` elem összegét vesszük. Ezt fel tudjuk írni zárt képlettel is:
`f_n=a_1·(q^n-1)/(q-1)=(3^n-1)/2`
Vagyis a hatvány-mátrix ez lett:
`A^n=(((3^n+1)/2,0,(3^n-1)/2),(0,1,0),((3^n-1)/2,0,(3^n+1)/2))`
`((f+1,0,f),(0,1,0),(f,0,f+1))`
Egyelőre ez csak sejtés, de n=1-re meg még további kis n-ekre is igaz. Teljes indukcióval be tudjuk látni, hogy minden n-re igaz. Ehhez elég annyi, hogy n=1-re igaz, feltesszük, hogy n-re is, aztán megnézzük n+1-re:
`((f+1,0,f),(0,1,0),(f,0,f+1))·((2,0,1),(0,1,0),(1,0,2))=(((f+1)·2+f,0,(f+1)+f·2),(0,1,0),(f·2+(f+1),0,f+(f+1)·2))`
`=((3f+2,0,3f+1),(0,1,0),(3f+1,0,3f+2))=((g+1,0,g),(0,1,0),(g,0,g+1))` ahol `g=3f+1`
Ez is tényleg olyan alakú mátrix, tehát teljes indukcióval beláttuk, hogy mindegyik hatvány ilyen alakú.
Ki kellene még találni, hogy mi `f` értéke az `n` függvényében. Láttuk, hogy `g=3f+1`, vagy máshogy írva: `f_(n+1)=3·f_n+1`
`f_1=1`
`f_2=3+1`
`f_3=3(3+1)+1=9+3+1`
`f_4=3(9+3+1)+1=27+9+3+1`
Szóval jó sok 3 hatványt kell összeadni.
Vagyis általánosan:
`f_n=sum_(k=0)^(n-1) 3^k`
ami egy mértani sorozat összege, ahol `a_1=1, q=3` és `n` elem összegét vesszük. Ezt fel tudjuk írni zárt képlettel is:
`f_n=a_1·(q^n-1)/(q-1)=(3^n-1)/2`
Vagyis a hatvány-mátrix ez lett:
`A^n=(((3^n+1)/2,0,(3^n-1)/2),(0,1,0),((3^n-1)/2,0,(3^n+1)/2))`
Módosítva: 7 éve
2
-
Törölt: Köszönöm nagyon nagyon! Örök hála
 7 éve
0
7 éve
0