Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Valaki megtudja ezt oldani?
 gabor199808
kérdése
gabor199808
kérdése
806
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Fizika
Válaszok
1 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
A kondenzátor feltöltődik a csúcsértékre (illetve majdnem, még lejön a dióda nyitófeszültsége), majd utána `RC` időállandóval kezd lecsengeni a következő félperiódusig.
Az ingadozás tehát :
`\Delta U=(U_\text{csúcs}-U_D)*(1-e^(-T/(RC)))``=``(U_\text{csúcs}-U_D)*(1-e^(-1/(fRC)))``=``(230*sqrt(2)-0.6)(1-exp(-1/(50*600*3300*10^-6)))~~3.3\text{V}`
Még egyszerűbb a számítás, ha az exponenciális függvényt a Taylor-sorának lineáris részével közelítjük (megtehetjük, mert kicsi az ingadozás), ekkor:
`\Delta U~~(U_\text{csúcs}-U_D)/(fRC)``=``(230sqrt(2)-0.6)/(50*600*3300*10^-6)~~3.3\text{V}`
Ennek a közepe:
`U_\text{ki,átl}=U_\text{csúcs}-U_D-(\Delta U)/2~~230sqrt(2)-0.6-3.3/2~~323\text{V}`
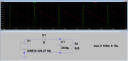
Ezek bevett közelítő számítások, az egzakt exponenciális lecsengés kiszámolása és az átlagérték kiintegrálása helyett kis ingadozás esetén ezek is jó eredményt adnak. Amint a mellékelt szimuláció mutatja, elég jó összhangban vannak a valósággal.
A képletek illusztrációja látható pl. ezen az ábrán (de vigyázz, az ábra kétutas egyenirányítóra vonatkozik): http://hyperphysics.phy-astr.gsu.edu/hbase/Electronic/ietron/ripple8.gif
Az ingadozás tehát :
`\Delta U=(U_\text{csúcs}-U_D)*(1-e^(-T/(RC)))``=``(U_\text{csúcs}-U_D)*(1-e^(-1/(fRC)))``=``(230*sqrt(2)-0.6)(1-exp(-1/(50*600*3300*10^-6)))~~3.3\text{V}`
Még egyszerűbb a számítás, ha az exponenciális függvényt a Taylor-sorának lineáris részével közelítjük (megtehetjük, mert kicsi az ingadozás), ekkor:
`\Delta U~~(U_\text{csúcs}-U_D)/(fRC)``=``(230sqrt(2)-0.6)/(50*600*3300*10^-6)~~3.3\text{V}`
Ennek a közepe:
`U_\text{ki,átl}=U_\text{csúcs}-U_D-(\Delta U)/2~~230sqrt(2)-0.6-3.3/2~~323\text{V}`
Ezek bevett közelítő számítások, az egzakt exponenciális lecsengés kiszámolása és az átlagérték kiintegrálása helyett kis ingadozás esetén ezek is jó eredményt adnak. Amint a mellékelt szimuláció mutatja, elég jó összhangban vannak a valósággal.
A képletek illusztrációja látható pl. ezen az ábrán (de vigyázz, az ábra kétutas egyenirányítóra vonatkozik): http://hyperphysics.phy-astr.gsu.edu/hbase/Electronic/ietron/ripple8.gif
0
- Még nem érkezett komment!