Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Telítési görbe a méréstechnikában
kcinti06
kérdése
911
Határozza meg közelítéssel egy telítési görbe szerint változó mérés szupremumát, ha a kezdeti érték 20°C, 10 mp múlva 50°C-ot, 20 mp múlva pedig 60°C-ot mérünk.
- Írja fel és ábrázolja a függvénykapcsolatot!
- Találjon az iterációhoz megfelelõ alsó és felsõ értéket!
- Táblázatkezelõvel vagy számológéppel közelítsen a megoldásra!
- Mennyi a függvény retardációs ideje?
Ameddig eljutottam: y1(fok):30, y2(fok): 40. Ami még a kérdés: y.sup(fok), tau(s), f.sup(fok).
- Írja fel és ábrázolja a függvénykapcsolatot!
- Találjon az iterációhoz megfelelõ alsó és felsõ értéket!
- Táblázatkezelõvel vagy számológéppel közelítsen a megoldásra!
- Mennyi a függvény retardációs ideje?
Ameddig eljutottam: y1(fok):30, y2(fok): 40. Ami még a kérdés: y.sup(fok), tau(s), f.sup(fok).
Jelenleg 1 felhasználó nézi ezt a kérdést.
fizika, görbe, méréstechnika, telítési
fizika, görbe, méréstechnika, telítési
0
Felsőoktatás / Fizika
Válaszok
1
AlBundy
{ Polihisztor }
válasza
Adhattál volna valami kontextust a feladathoz (milyen tárgy, mit jelöltél y-nal), mert ez valami elég speciális terminológia. Ezek hiányában a következő megoldást tudom adni:
A mért `x` mennyiség az alábbi függvény szerint változik:
`x(t)=(x_\text{sup}-x_0)(1-e^(-t/\tau))+x_0`
Ahol `tau` a retardációs idő (vagy gyakoribb nevén időállandó), `x_\text{sup}` a szuprémum (ehhez tart `x` a végtelenben: `x_\text{sup}=lim_{t->infty}x(t)`), az `x_0` pedig a kezdeti érték (`x_0=x(0)`).
A kezdeti értéket megadták: `x_0=20\text{°C}`, a kérdés `x_\text{sup}` és `tau`. Erre a két ismeretlenre van két egyenletünk, tehát elvileg megoldható.
Helyettesítsük be a megadott adatokat:
`50=(x_\text{sup}-20)(1-e^(-10/tau))+20`
`60=(x_\text{sup}-20)(1-e^(-20/tau))+20`
Vonjuk ki a 20-at, és osszunk le az exponenciális taggal:
`30/(1-e^(-10/tau))=x_\text{sup}-20`
`40/(1-e^(-20/tau))=x_\text{sup}-20`
Ezek szerint:
`30/(1-e^(-10/tau))=40/(1-e^(-20/tau))`
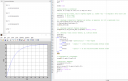
Ha ezt az egyenletet megoldjuk, megkapjuk `tau`-t. A feladat számítógépes, iteratív megoldásról beszél, de ez fölösleges, analitikusan is megy. Mindenesetre mellékeltem hozzá egy MATLAB szkriptet képként. Ha nem ismered a MATLAB-ot, valamennyire akkor is érthető szerintem, elég olvasható nyelv. Az analitikus megoldás egyszerű:
`3-3e^(-20/tau)=4-4e^(-10/tau)`
`3e^(-20/tau)-4e^(-10/tau)+1=0`
`3a^2-4a+1=0`
Az `a=e^(-10/tau)` segédváltozó bevezetésével másodfokú egyenletet kaptunk, aminek a megoldásai `a=1` és `a=1/3`. Az előbbi nem jó (ahhoz végtelen időállandó tartozna), utóbbi viszont igen:
`e^(-10/tau)=1/3`
`10/tau=ln3`
`tau=10/ln3~~9.102\text{s}`
Tehát a retardációs idő megvan, ebből meg már bármelyik egyenlet alapján visszaszámolható a szuprémum:
`x_\text{sup}=30/(1-1/3)+20=65\text{°C}`
Vagyis a függvénykapcsolat a következő (ha `x`-et °C-ban, `t`-t pedig másodpercben mérjük):
`x(t)=45(1-e^(-t/9.102))+20`
Mellékeltem képet is a függvényről.
A mért `x` mennyiség az alábbi függvény szerint változik:
`x(t)=(x_\text{sup}-x_0)(1-e^(-t/\tau))+x_0`
Ahol `tau` a retardációs idő (vagy gyakoribb nevén időállandó), `x_\text{sup}` a szuprémum (ehhez tart `x` a végtelenben: `x_\text{sup}=lim_{t->infty}x(t)`), az `x_0` pedig a kezdeti érték (`x_0=x(0)`).
A kezdeti értéket megadták: `x_0=20\text{°C}`, a kérdés `x_\text{sup}` és `tau`. Erre a két ismeretlenre van két egyenletünk, tehát elvileg megoldható.
Helyettesítsük be a megadott adatokat:
`50=(x_\text{sup}-20)(1-e^(-10/tau))+20`
`60=(x_\text{sup}-20)(1-e^(-20/tau))+20`
Vonjuk ki a 20-at, és osszunk le az exponenciális taggal:
`30/(1-e^(-10/tau))=x_\text{sup}-20`
`40/(1-e^(-20/tau))=x_\text{sup}-20`
Ezek szerint:
`30/(1-e^(-10/tau))=40/(1-e^(-20/tau))`
Ha ezt az egyenletet megoldjuk, megkapjuk `tau`-t. A feladat számítógépes, iteratív megoldásról beszél, de ez fölösleges, analitikusan is megy. Mindenesetre mellékeltem hozzá egy MATLAB szkriptet képként. Ha nem ismered a MATLAB-ot, valamennyire akkor is érthető szerintem, elég olvasható nyelv. Az analitikus megoldás egyszerű:
`3-3e^(-20/tau)=4-4e^(-10/tau)`
`3e^(-20/tau)-4e^(-10/tau)+1=0`
`3a^2-4a+1=0`
Az `a=e^(-10/tau)` segédváltozó bevezetésével másodfokú egyenletet kaptunk, aminek a megoldásai `a=1` és `a=1/3`. Az előbbi nem jó (ahhoz végtelen időállandó tartozna), utóbbi viszont igen:
`e^(-10/tau)=1/3`
`10/tau=ln3`
`tau=10/ln3~~9.102\text{s}`
Tehát a retardációs idő megvan, ebből meg már bármelyik egyenlet alapján visszaszámolható a szuprémum:
`x_\text{sup}=30/(1-1/3)+20=65\text{°C}`
Vagyis a függvénykapcsolat a következő (ha `x`-et °C-ban, `t`-t pedig másodpercben mérjük):
`x(t)=45(1-e^(-t/9.102))+20`
Mellékeltem képet is a függvényről.
Módosítva: 7 éve
0
- Még nem érkezett komment!