Biztosan `f(x)=cos(pi^x)` a függvény? Szerintem `f(x)=cos(pi x)` lesz az.



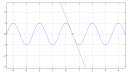
A függvényünk `f(x)=cos(pi x)`, ennek keressük az `x=1/2` helyen az érintőjét. Itt a függvény az `f(1/2)=cos(pi/2)=0` értéket veszi fel, tehát az érintő az `(1/2; 0)` ponton fog áthaladni.

A függvény deriváltja `f'(x)=-pi sin(pi x)`, ennek értéke az `x=1/2` helyen `m=f'(1/2)=-pi sin(pi/2)=-pi`, ez lesz az érintő meredeksége.

Tehát keressük azt az `e(x)=-pi x+b` egyenest, amely átmegy az `(1/2; 0)` ponton:

`0=-pi*1/2+b`

Az egyenletet megoldva azt kapjuk, hogy `b=pi/2`, tehát a keresett értintő `e(x)=-pi x+pi/2`.



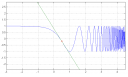
Ha netán mégis a csúnya `f(x)=cos(pi^x)` függvényről van szó, akkor az érintési pont `(1/2; cos sqrt(pi))`, a derivált `f'(x)=-pi^x sin(pi^x) ln(pi)`, a meredekség `m=-sqrt(pi) ln(pi) sin sqrt(pi)`, a tengelymetszet `b=cos sqrt(pi)+1/2 sqrt(pi) ln(pi) sin sqrt(pi)`.