Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Valószínűségszámítás
 Handsome Matthew
kérdése
Handsome Matthew
kérdése
655
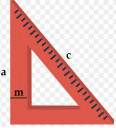
Az alábbi favonalzóra véletlenszerűen rádobunk egy vasgolyót. Mekkora a valószínűsége, hogy a golyóval a közepén lévő lyukat találjuk el, ha a vonalzó külső méretei:
a = 50 cm,
c = 100 cm,
és a vastagsága mindenütt 5 cm?
m = 5 cm.
a = 50 cm,
c = 100 cm,
és a vastagsága mindenütt 5 cm?
m = 5 cm.
Jelenleg 1 felhasználó nézi ezt a kérdést.
Matematika, valószínűségszámítás, trigonometria
Matematika, valószínűségszámítás, trigonometria
0
Középiskola / Matematika
Válaszok
2 Handsome Matthew
válasza
Handsome Matthew
válasza
Kiindulás a feladat megoldásához:
- A másik befogó hosszának kiszámítása (Pitagorasz-tétel)
- Az eredeti háromszög területének kiszámítása (Háromszög területe)
- Az eredeti háromszög területe, és a megadott vastagság alapján a kisebb háromszög oldalainak, majd területének kiszámítása (?)
- Az eredeti háromszög területe - összes eset
- A kisebb háromszög területe - kedvező eset
P(A) = kedvező / összes
Mint látható, a gondot az utolsó előtti, harmadik lépés okozza, ugyanis nem tudok mi alapján kiindulni.
- A másik befogó hosszának kiszámítása (Pitagorasz-tétel)
- Az eredeti háromszög területének kiszámítása (Háromszög területe)
- Az eredeti háromszög területe, és a megadott vastagság alapján a kisebb háromszög oldalainak, majd területének kiszámítása (?)
- Az eredeti háromszög területe - összes eset
- A kisebb háromszög területe - kedvező eset
P(A) = kedvező / összes
Mint látható, a gondot az utolsó előtti, harmadik lépés okozza, ugyanis nem tudok mi alapján kiindulni.
0
- Még nem érkezett komment!
 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
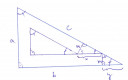
Nézd meg a mellékelt képet! Ha behúzod ezeket a vonalakat, akkor az azonosan jelölt szögek egyenlősége miatt hasonló háromszögek keletkeznek. Tehát maga az egész vonalzó, a belső "lyuk", valamint a vonalak behúzásával kapott kicsi háromszögek mind hasonlóak egymáshoz. Emiatt `x/m=c/a`, vagyis `x=mc/a=5*100/50=10` cm. Ugyanígy `y/m=b/a`, vagyis `y=mb/a=5sqrt3` cm. Tehát a belső háromszög "alsó" befogójának hosszúsága `b-m-x-y=45sqrt3-15~~62.94` cm.
A belső háromszög így megkapott oldala a nagy háromszög b oldalának felel meg. Tehát a hasonlósági arány köztük `lambda=(45sqrt3-15)/(50sqrt3)=(9-sqrt3)/10~~0.727`. A kis háromszög területe a nagy területének `\lambda^2`-szerese, azaz kb. `52.82%`-a.
A belső háromszög így megkapott oldala a nagy háromszög b oldalának felel meg. Tehát a hasonlósági arány köztük `lambda=(45sqrt3-15)/(50sqrt3)=(9-sqrt3)/10~~0.727`. A kis háromszög területe a nagy területének `\lambda^2`-szerese, azaz kb. `52.82%`-a.
Módosítva: 7 éve
0
- Még nem érkezett komment!