Körszelet

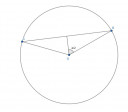
Rajzoltam egy hevenyészett ábrát.
A feladat meghatározása szerint OC=OB=20 cm, CB=24 cm!
Az ábrán berajzolt α/2 és rajta keresztül α szöget kétféleképpen lehet kiszámolni.
1) sin(α/2)=(szöggel szembeni befogó/átfogó) => sin(α/2)=12/20 => sin(α/2)=0,6 => α/2=36,87° => α=73,74°
2) Ha már tanultátok, akkor a koszinusz tételt is használhatjuk: c²=a²+b²-2ab*cos(α) => 24²=20²+20²-2*20*20*cos(α) => 576=800-800*cos(α) => (576-800)/(-800)=cos(α) => cos(α)=0,28 => α=73,74°
A mindkét körszelet kerületéhez ismernünk kell az α, illetve a másik oldalon lévő (360°-α) szöghöz tartozó ívhosszt.
i=α*(r*π)/180°
CB₁ ívhossz: 73,74*(20*π)/180=25,74 (cm)
CB₂ ívhossz: 286,26*(20*π)/180=99,92 (cm) Nyilván a kör teljes kerületéből kivont előző eredmény is ide vezet (2rπ => 2*20*π=125,66 => 125,66-25,74=99,92).
Tehát az egyik körszelet kerülete: 25,74+24=49,74 (cm), míg a másik 99,92+24=123,92 (cm).

A terület kiszámítása már egy kicsit bonyolultabb.
Itt a körcikkből indulunk ki, majd egyik esetben kivonjuk, a másik esetben hozzáadjuk az BOC háromszög területét.
Az ábrán berajzolt magasság Pitagorasz segítségével kiszámolható: 20²-12²=m² => m=16 (cm)!
TBOC háromszög=24*16/2 => TBOC háromszög=192 (cm²)

A körcikk területét a már kiszámolt ívhossz számoljuk tovább: T=i*r/2
Tkörcikk=25,74*20/2=257,4 (cm²)
Ebből kell levonni a háromszög területét:
Tkörszelet=Tkörcikk-TBOC háromszög => Tkörszelet=257,4-192=65,4(cm²)
A másik körszelet:
Tkörcikk=99,92*20/2=999,24 (cm²)
Ehhez az eredményhez viszont hozzá kell adni a háromszög területét:
Tkörszelet=Tkörcikk+TBOC háromszög => Tkörszelet=999,24+192=1191,24(cm²)
Ugyan ide jutottunk volna, ha a teljes kör területéből kivontuk volna ez előző eredményünket (r²*π => 20²*π=1256,64 => 1256,64-65,4=1191,24 (cm²)