Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Hányféleképpen lehet?
 Törölt
kérdése
Törölt
kérdése
2330
Sziasztok! Valaki segítene ebben a feladatokban, mert sehogy sem tudom megoldani. Köszönöm szépen a válaszokat! 
1.) A család autóban ül. Elől ül anya és apa, hátul a három gyerek. Hányféleképpen helyezkedhetnek el a kocsiban, ha anyának és apának is van jogosítványa?
2.) A születésnapi ebédnél a család nyolc tagja egy asztal köré ült. Hány különböző módon ülhettek le, ha dédmama az asztalfőn foglalt helyet, jobbján Csilla, balján pedig Hajni ült?
3.) Hány átló húzható egy konvex 16 szögben?
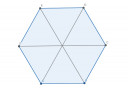
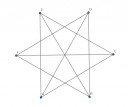
4.) Hat település mindegyikéből pontosan három másik településre lehet eljutni közvetlen, egyenes műúton. Hány közvetlen út vezet a települések között? Rajzolj egy lehetséges esetet!
5.) Számítsd ki, hogy mennyi 4!; 5!; 6!; 7!; 8!; 9!; 10!
Kérem szépen, hogy segítsen valaki, mert nagyon nem értem.

1.) A család autóban ül. Elől ül anya és apa, hátul a három gyerek. Hányféleképpen helyezkedhetnek el a kocsiban, ha anyának és apának is van jogosítványa?
2.) A születésnapi ebédnél a család nyolc tagja egy asztal köré ült. Hány különböző módon ülhettek le, ha dédmama az asztalfőn foglalt helyet, jobbján Csilla, balján pedig Hajni ült?
3.) Hány átló húzható egy konvex 16 szögben?
4.) Hat település mindegyikéből pontosan három másik településre lehet eljutni közvetlen, egyenes műúton. Hány közvetlen út vezet a települések között? Rajzolj egy lehetséges esetet!
5.) Számítsd ki, hogy mennyi 4!; 5!; 6!; 7!; 8!; 9!; 10!
Kérem szépen, hogy segítsen valaki, mert nagyon nem értem.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 csettlik
megoldása
csettlik
megoldása
1) A szülők előre kétféleképpen tudnak beülni, mivel mindkettőjüknek van jogosítványa (bár az autó üzemanyaggal megy nem jogosítvánnyal) 
Ez a két lehetőség: anya vezet-apa anyósülés, vagy apa vezet-anya a jobb egyben ül.
A gyerekek hatféleképpen tudnak beülni hátulra. A bal hátsó ülésre választhatok három gyereket, a középsőre már csak kettőt, míg a jobb hátsóra már csak egyet. 3*2*1 => 6.
Mivel a szülők kétféleképpen tudnak beülni, így az összes lehetőség: 2*3! (olvasd kétszer három faktoriális) Összesen 12.
2.)
A Dédit, Csillát és Hajnit tekintsük egy egységnek. Hogy az asztal melyik vége az asztalfő, az kérdés, így én úgy tekintem, hogy Dédi ülhet A végén és B végén is. Ezt ugye két eset!
Mivel további korlát nincs így a helyeket egy sorba rendezném.
Első helyre 5 embert tudok kiválasztani, a második helyre már csak 4-et, és így tovább. Így az öt ember 5*4*3*2*1 (5!=120) féleképpen tudom leültetni.
Az asztal végét két különböző esetnek véve a teljes szám 2*5*4*3*2*1 => 240.
3)
Egy n oldalú sokszög egyik csúcsából n-3 átló húzható, hiszen nem tudok saját magába, és a két szomszédos csúcsba húzni átlót. Mivel Minden csúcsból ugyan annyi átló húzható, ezért az összes átlók száma n*(n-3)! Igen ám, de így kétszer számoltam az átlókat, mert számoltam innen oda és megszámoltam amikor onnan ide húztam. Ezért el kell osztanom kettővel az eredményt.
Ha most n=16, akkor az összeges átló: 16*(16-3)/2=104 átló!
4)
Lásd ábrákat!
Nekem 9-ből sikerült megoldani! 6 falu * 3 út = 18. De itt is kétszer számoltam, hogy A-ból mentem B-be, illetve B-ből mentem A-ba! Így 6*3/2=9.
5)
4!=4*3*2*1 =24
5!=5*4*3*2*1 =5*4!=5*24=120
6!=6*5*4*3*2*1=6*5!=6*120=720
7!=7*6*5*4*3*2*1=7*6!=7*720=5040
8!=8*5040=40320
9!=9*40320=362880
10!=10*362880=3628800

Ez a két lehetőség: anya vezet-apa anyósülés, vagy apa vezet-anya a jobb egyben ül.
A gyerekek hatféleképpen tudnak beülni hátulra. A bal hátsó ülésre választhatok három gyereket, a középsőre már csak kettőt, míg a jobb hátsóra már csak egyet. 3*2*1 => 6.
Mivel a szülők kétféleképpen tudnak beülni, így az összes lehetőség: 2*3! (olvasd kétszer három faktoriális) Összesen 12.
2.)
A Dédit, Csillát és Hajnit tekintsük egy egységnek. Hogy az asztal melyik vége az asztalfő, az kérdés, így én úgy tekintem, hogy Dédi ülhet A végén és B végén is. Ezt ugye két eset!
Mivel további korlát nincs így a helyeket egy sorba rendezném.
Első helyre 5 embert tudok kiválasztani, a második helyre már csak 4-et, és így tovább. Így az öt ember 5*4*3*2*1 (5!=120) féleképpen tudom leültetni.
Az asztal végét két különböző esetnek véve a teljes szám 2*5*4*3*2*1 => 240.
3)
Egy n oldalú sokszög egyik csúcsából n-3 átló húzható, hiszen nem tudok saját magába, és a két szomszédos csúcsba húzni átlót. Mivel Minden csúcsból ugyan annyi átló húzható, ezért az összes átlók száma n*(n-3)! Igen ám, de így kétszer számoltam az átlókat, mert számoltam innen oda és megszámoltam amikor onnan ide húztam. Ezért el kell osztanom kettővel az eredményt.
Ha most n=16, akkor az összeges átló: 16*(16-3)/2=104 átló!
4)
Lásd ábrákat!
Nekem 9-ből sikerült megoldani! 6 falu * 3 út = 18. De itt is kétszer számoltam, hogy A-ból mentem B-be, illetve B-ből mentem A-ba! Így 6*3/2=9.
5)
4!=4*3*2*1 =24
5!=5*4*3*2*1 =5*4!=5*24=120
6!=6*5*4*3*2*1=6*5!=6*120=720
7!=7*6*5*4*3*2*1=7*6!=7*720=5040
8!=8*5040=40320
9!=9*40320=362880
10!=10*362880=3628800
1
-
Törölt: Nagyon szépen köszönöm!
 7 éve
0
7 éve
0