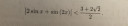Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Egyenlet
 Dpeter99
kérdése
Dpeter99
kérdése
534
Igazoljuk, hogy
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 bongolo
{
bongolo
{  }
megoldása
}
megoldása
Rég volt már ez a kérdésed, de hátha érdekes még...
Csak az a megoldás jut hirtelen eszembe, hogy nézzük meg, mikor van szélsőértéke a szinuszos összegnek. Vagyis mikor nulla a deriváltja?
`2cosx+2cos(2x)=0`
`cosx+2cos^2x-1=0`
ami ugyanaz, mint `2u^2+u-1=0`
`u_(1,2)=(-1+-sqrt(1+8))/4`
`cosx_1 = 1/2\ \ \ \ \ \ \ \ \ \ ` → `x_1=+-π/3+2kπ`
`cosx_2 = "-1"\ \ \ \ \ \ \ \ \ \ ` → `x_2=+-π+2kπ`
Ezeken a helyeken lehet szélsőértéke a `2sinx+sin2x` kifejezésnek. Egyszerű behelyettesítéssel kijön, hogy mi ez az érték:
`sin(x_1)=+-sqrt3/2`
`sin(2x_1)=+-sqrt3/2`
`|2sinx_1+sin2x_1|=(3sqrt3)/2`
`sin(x_2)=0`
`sin(2x_2)=0`
Ebből 0 jön ki. Egyébként ezen a helyeken nem szélsőértéke, hanem inflexiós pontja van a függvénynek, de ez nem igazán számít...
Már csak azt kell belátni, hogy
`(3sqrt3)/2 < (3+2sqrt2)/2`
emeljük négyzetre
`9·3 < 9+2·3·2sqrt2+4·2`
`27 < 17+12sqrt2`
ami bőven igaz.
Biztos van valamilyen elemi megoldása is, de nem jövök rá...
Csak az a megoldás jut hirtelen eszembe, hogy nézzük meg, mikor van szélsőértéke a szinuszos összegnek. Vagyis mikor nulla a deriváltja?
`2cosx+2cos(2x)=0`
`cosx+2cos^2x-1=0`
ami ugyanaz, mint `2u^2+u-1=0`
`u_(1,2)=(-1+-sqrt(1+8))/4`
`cosx_1 = 1/2\ \ \ \ \ \ \ \ \ \ ` → `x_1=+-π/3+2kπ`
`cosx_2 = "-1"\ \ \ \ \ \ \ \ \ \ ` → `x_2=+-π+2kπ`
Ezeken a helyeken lehet szélsőértéke a `2sinx+sin2x` kifejezésnek. Egyszerű behelyettesítéssel kijön, hogy mi ez az érték:
`sin(x_1)=+-sqrt3/2`
`sin(2x_1)=+-sqrt3/2`
`|2sinx_1+sin2x_1|=(3sqrt3)/2`
`sin(x_2)=0`
`sin(2x_2)=0`
Ebből 0 jön ki. Egyébként ezen a helyeken nem szélsőértéke, hanem inflexiós pontja van a függvénynek, de ez nem igazán számít...
Már csak azt kell belátni, hogy
`(3sqrt3)/2 < (3+2sqrt2)/2`
emeljük négyzetre
`9·3 < 9+2·3·2sqrt2+4·2`
`27 < 17+12sqrt2`
ami bőven igaz.
Biztos van valamilyen elemi megoldása is, de nem jövök rá...
0
- Még nem érkezett komment!