Térgeometria

Legyenek a téglatest méretei `a ≤ b ≤ c`.

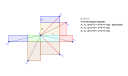
Két pont között a legrövidebb utat úgy tudjuk megszerkeszteni, hogy kiterítjük a téglatest hálóját, és a két pont között egyenest húzunk. Az egyenes nem mehet ki a hálóból!

Az első ábra a téglatest kiterített hálója, de oly módon, hogy a piros, kék és barna színű oldallap mindegyike két helyre is ki van terítve látszólag. Természetesen csak az egyik van benne a hálóban: ha pl. elhagyod azt a három oldallapot, amik az `A_1, A_2` és `A_5` pontokat tartalmazzák, akkor egy szokásos módon kiterített hálót kapunk. A három megduplázott oldallapnak az a célja, hogy némelyik berajzolt egyenes ne menjen ki a hálóból.

Egy hálón az eredeti téglatest némelyik pontja több helyen is megtalálható. Pl. a síkbeli `A_1, A_2, A_3, A_4, A_5` és `A_6` pontok a térben mind ugyanaz az egyetlen pont, mégpedig az `A` ponttal szemközti pont. Azt a legrövidebb útvonalat keressük, ami összeköti az `A` pontot valamelyik `A_x` ponttal. Az `A` pontból a pontot meghatározó 3 oldalsík bármelyike mentén el tudunk indulni, majd az `A`-val szemközti 2 él valamelyikét metszve jutunk a testátló szemközti végpontjába, `A_x`-be. Ez összesen 6-féle út, mindegyik látszik az ábrán.

A távolságok négyzetei a Pitagorasz tétellel számolhatóak (lásd az ábrát). Mind a hat esetben `a^2+b^2+c^2+2xy` alakúak, ahol `x` és `y` azon oldalélek, amiket nem metszett az útvonal. Annak a két oldalélnek az összege adja ugyanis a Pitagorasz háromszög egyik befogóját, a másikat pedig a metszett él. Ezért a legrövidebb távolságot akkor kapjuk, amikor az útvonal metszi a leghosszabb `c` oldalt.

Fontos észrevétel, hogy két legrövidebb útvonal is van, mert a téglatest bármelyik pontjába futó élek egyike a `c` oldalél, ami két oldalsík metszete. Mindkét ezen oldalsíkon elindulva, majd az oldallap másik `c` oldalélét metszve ugyanakkora minimális távolságot kapunk.

A többi útvonallal a jövőben nem foglalkozunk, csak a két legrövidebbel.

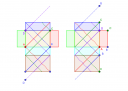
A második ábrán a bal oldali testháló azt az esetet mutatja, amikor a négy pont olyan oldallapon van, aminek egyik éle a leghosszabb `c` oldal. A négy pont négyféle színnel van jelölve, a belőle induló legrövidebb utak is ugyanolyan színűek. Az utak az előzőekben leírtak szerint a `c` oldalél metszésével jutnak el a szemközti pontokba.
Akár a folytonos, akár a szaggatott vonal-négyest választjuk, azok az utak párhuzamosak egymással, mert a háló négy kiterített oldallapjának `c` élei párhuzamosak és felváltva `a` és `b` távolságokra vannak egymástól. Vagyis azokon haladva a hangyák el tudják kerülni egymást.
(Az ábrán a `D` pontból induló útvonal pontozott vonalrésze alul folytatódik. Természetesen a hálón ez is egyenes vonal, csak most nem dupláztam meg az alsó barna oldallapot.)

A jobb oldali háló azt az esetet mutatja, mikor a négy ABCD pont olyan oldallapon van, aminek egyik oldala sem `c` hosszú. Ekkor az ábra szerinti `B` és `C` pontok a térbeli téglatesten valójában ugyanazok a pontok, amiket szintén `B`-vel illetve `C`-vel jelöltem a hálón. Vagyis a négy pont egy egyenesben van, és ugyanazok az utak a legrövidebbek, mint a bal oldali ábránál is (csak most más a színük...) Vagyis ilyenkor is át tudnak menni a hangyák párhuzamos utakon.