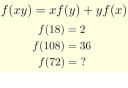Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Egy számolós feladvány
 gyula205
kérdése
gyula205
kérdése
89
Lásd a csatolt képet
A forrás: https://hu.pinterest.com/pin/536983955594337565/
A forrás: https://hu.pinterest.com/pin/536983955594337565/
Jelenleg 1 felhasználó nézi ezt a kérdést.
logika, egyenlet
logika, egyenlet
0
Felsőoktatás / Matematika
Válaszok
2 Ákos2
megoldása
Ákos2
megoldása
vegyünk fel egy új függvényt g(x)=f(x)/x Ezt vissza kell helyettesíteni, így:
x*y*g(xy)=x*y*(g(x)+g(y)) Ezen a ponton x*y-al lehet egyszerűsíteni:
g(xy)=g(x)+g(y)
Ezen a ponton tételezzük fel, hogy x és y egész számok, ebben az esetben az alábbi prímkitevős felbontás írható fel:
g(n)=A*v(n)+B*u(n) ezt vissza lehet értelmezni f(n)= n*(A*v(n)+B*u(n)).
Itt kell felhasználni az ismert értékeket, ugyanis:
18=(2^1)*(3^2)
108=(2^2)*(3^3)
72= (2^3)*(3^2)
Itt A= 2^x hatványkitevő és B=3^y-ikon hatványkitevő, amiből az alábbi egyenleteket kapjuk:
18(A+2B)=2
108(2A+3B)= 36.
Ennek a kétismeretlenes egyenletrendszernek a megoldásával nem húzom az időt, A=1/3, B=-1/9
f(72)= 72(3A+2B)=72*((1/3)*3+2*(-1/9))=72(1-(2/9))=56
f(72)=56
x*y*g(xy)=x*y*(g(x)+g(y)) Ezen a ponton x*y-al lehet egyszerűsíteni:
g(xy)=g(x)+g(y)
Ezen a ponton tételezzük fel, hogy x és y egész számok, ebben az esetben az alábbi prímkitevős felbontás írható fel:
g(n)=A*v(n)+B*u(n) ezt vissza lehet értelmezni f(n)= n*(A*v(n)+B*u(n)).
Itt kell felhasználni az ismert értékeket, ugyanis:
18=(2^1)*(3^2)
108=(2^2)*(3^3)
72= (2^3)*(3^2)
Itt A= 2^x hatványkitevő és B=3^y-ikon hatványkitevő, amiből az alábbi egyenleteket kapjuk:
18(A+2B)=2
108(2A+3B)= 36.
Ennek a kétismeretlenes egyenletrendszernek a megoldásával nem húzom az időt, A=1/3, B=-1/9
f(72)= 72(3A+2B)=72*((1/3)*3+2*(-1/9))=72(1-(2/9))=56
f(72)=56
0
-
gyula205: A bizonyítás menete nem teljesen világos a számomra. Szerintem nem prímkitevős, hanem 2 illetve 3 alapú egész kitevős hatványokkal van dolgunk. A g(n) függvény kifejtésében nem látszik világosan hogyan függnek v és u függvények n-től? 3 hete 0
-
Ákos2: Prímkitevős alatt azt értettem, hogy az egyes egzakt értékeknek az adott behelyettesítési értéken a prímtényezős felbontásának az egyes komponensek (2,3 ebben az esetben) kell venni a hatványkitevőit. 3 hete 0
-
Ákos2: g(n)=A*v(n)+B*v(n) pedig egy általános alak, ez már inkább elmélet, de a lényeg az, hogy a g(n) függvény mindig felbontható a prímtényezős hatványkitevők felbontása szerint. Ebben a feladatban az egyetlen "kacifántos" rész az hogy trükközni kell az f(x)/x=g(x) és ennek a visszalakításával. Remélem így tisztább 3 hete 0
-
gyula205: Például a 11-edik sorban az v(18)=1 és u(18)=2 vagy a 12-edik sorban v(108)=2 és u(108)=3. Miért? Inkább nem arról van szó, hogy az f(x) értelmezési tartományában `2^xi*3^eta` alakú egész számok vannak? 3 hete 0
-
gyula205: Ahol `xi` és `eta` egész szám. A kapott f(72)=56 végeredmény jó, de egyenlőre hamis vágányon vagyunk. 3 hete 0
-
gyula205: Triviálisan következnek, hogy `f(1)=0`; `f(4)=4*f(2)`; `f(6)=2*f(3)+3*f(2)`; `f(9)=6*f(3)`. Az egyenletrendszer felírását `f(2)` és `f(3)`-ra javaslom. 3 hete 0
-
gyula205: Fogalmam sincs, hogy számoltad ki az együtthatóidat, az így kapott egyenletrendszer megoldása elvisz a megoldáshoz. Nem muszáj "trükközni " a megoldáshoz. Akkor kapunk egy másik megoldást is. Kövesd tovább a fenti gondolatmenetet. `f(12)=12*f(2)+4*f(3)`, `f(18)=6*f(3)+3*f(6)=12*f(3)+9*f(2)=2` ez az egyik egyenlet; `f(108)=6*f(18)+18*f(6)=108*(f(2)+f(3))=36` ez a másik egyenlet. 2 hete 0
-
gyula205: Az egyenletrendszer megoldása `f(2)=2/3` és `f(3)=-1/3`. Befejezésül `f(72)=4*f(18)+18*f(4)=4*2+18*4*(2/3)=8+48=56`. 2 hete 0
 gyula205
válasza
gyula205
válasza
A fenti bizonyításban van egy kis elírás, mert `A=1/3` nem írható fel 2 hatványaként. A 10-edik sorban `A=g(2)` és `B=g(3)`. Tehát `g(2) `és `g(3)` lineáris kombinációjával fejezhető ki `g(18)` és `g(108)` is. Az ehhez vezető út lett itt "elbagatelizálva", ami nem annyira triviális. `g(4)=2*g(2)`; `g(6)=g(2)+g(3)`; `g(18)=g(3)+g(6)=1*g(2)+2*g(3)=A+2B`, ami a bizonyítás 11-edik sora.
`g(36)=2*g(6)=2(g(2)+g(3)`; `g(108)=g(3)+g(36)=2*g(2)+3*g(3)=2A+3B`, ami a bizonyítás 12-edik sorában olvasható.
Az egyenletrendszer megoldása (`A=1/3 és B=-1/9`) után le kell vezetni `g(72)` együtthatóit is.
`g(72)=g(2)+g(36)=3*g(2)+2*g(3)=3A+2B`. Szerintem így lesz érthetőbb a gyengébbek számára is a fenti megoldás.
Ajánlanám az olvasók számára, hogy a fenti megoldás komment részében írtam egy másik megoldásról is, ami nem használ fel semmilyen trükköt.
`g(36)=2*g(6)=2(g(2)+g(3)`; `g(108)=g(3)+g(36)=2*g(2)+3*g(3)=2A+3B`, ami a bizonyítás 12-edik sorában olvasható.
Az egyenletrendszer megoldása (`A=1/3 és B=-1/9`) után le kell vezetni `g(72)` együtthatóit is.
`g(72)=g(2)+g(36)=3*g(2)+2*g(3)=3A+2B`. Szerintem így lesz érthetőbb a gyengébbek számára is a fenti megoldás.
Ajánlanám az olvasók számára, hogy a fenti megoldás komment részében írtam egy másik megoldásról is, ami nem használ fel semmilyen trükköt.
Módosítva: 2 hete
0
- Még nem érkezett komment!