Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Derékszögű háromszög és körszelet.
_Gál_Levente_
kérdése
68
Számítsa ki annak a körszeletnek a területét melyet egy olyan körből szeltünk le amit egy 61 cm átfogó hosszúságú derékszögű háromszög köré írtunk és a körszelet íve a rövidebbik befogóval szemben helyezkedik el. Azt tudjuk, hogy a háromszög területe 330 cm².
Feladatok:
Határozzuk meg a két befogó hosszát.
Határozzuk meg a körszelet területét.
Feladatok:
Határozzuk meg a két befogó hosszát.
Határozzuk meg a körszelet területét.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1
kazah
válasza
`T=(ab)/2` = 330 `cm^2` `to` `ab=660`
`a^2+b^2=61^2`
`a^2+2ab+b^2` = `61^2+2*660` = 5041 = `(a+b)^2`
`a+b=root()(5041)` = 71
`a(71-a)=660`
`a^2-71a+660=0`
`a_(1,2)=(71 pm root()(71^2-4*660))/2` = `(71 pm 49)/2`
Az oldalak hossza tehát 60 és 11 cm.
A kör átmérője az átfogó, a sugár tehát 30,5 cm.
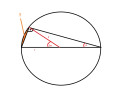
Ábra.
`tanalpha=11/60` `to` `alpha` = 10,39°
`2*alpha` = 20,78°
A körcikkből kivonjuk a háromszög területét.
Körcikk: `r^2*pi*(2alpha)/360`
Háromszög: `r^2*sin(2alpha)/2`
T = `30.5^2*3.14*20.78/360-30.5^2*sin(20.78)/2` = 3,67 `cm^2`
`a^2+b^2=61^2`
`a^2+2ab+b^2` = `61^2+2*660` = 5041 = `(a+b)^2`
`a+b=root()(5041)` = 71
`a(71-a)=660`
`a^2-71a+660=0`
`a_(1,2)=(71 pm root()(71^2-4*660))/2` = `(71 pm 49)/2`
Az oldalak hossza tehát 60 és 11 cm.
A kör átmérője az átfogó, a sugár tehát 30,5 cm.
Ábra.
`tanalpha=11/60` `to` `alpha` = 10,39°
`2*alpha` = 20,78°
A körcikkből kivonjuk a háromszög területét.
Körcikk: `r^2*pi*(2alpha)/360`
Háromszög: `r^2*sin(2alpha)/2`
T = `30.5^2*3.14*20.78/360-30.5^2*sin(20.78)/2` = 3,67 `cm^2`
1
- Még nem érkezett komment!