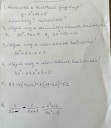Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Segítség matek
 máté2009
kérdése
máté2009
kérdése
236
Segítséget szeretnék kérni a mellékelt feladatok megoldásában. Nagy szépen köszönöm.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
3 AG495
megoldása
AG495
megoldása
2. a)
`5x^2-7x=0`
`x(5x-7)=0`
Szorzat akkor lehet nulla, ha egyik tényezője nulla:
`x(5x-7)=0`
`x_1=0`
`5x-7=0`
`x_2=7/5="1,4"`
2. b)
`2x^2-50=0`
`2x^2=50`
`x^2=25`
`x_1=5`
`x_2=-5`
3.
`3x^2+5x-2=0`
Alkalmazod a megoldóképletet:
`x={-5±sqrt{5^2+4*2*3}}/6={-5±sqrt{25+24}}/6={-5±sqrt49}/6={-5±7}/6`
`x_1={-5+7}/6=2/6=1/3`
`x_2={-5-7}/6=-2`
4.
`4x^4-37x^2+9=0`
Ez az egyenlet x²-re nézve másodfokú.
`x^2={37±sqrt{37^2-4*4*9}}/8={37±sqrt{1369-144}}/8={37±sqrt1225}/8={37±35}/8`
`x_1^2={37+35}/8=9`
`x_2^2={37-35}/8="0,25"`
Még tovább kell folytatni:
`x_1^2=9`
`x_11=3`
`x_12=-3`
`x_2^2="0,25"`
`x_21="0,5"`
`x_22=-"0,5"`
Ezt `x^2=y` helyettesítéssel is megoldhatod.
`5x^2-7x=0`
`x(5x-7)=0`
Szorzat akkor lehet nulla, ha egyik tényezője nulla:
`x(5x-7)=0`
`x_1=0`
`5x-7=0`
`x_2=7/5="1,4"`
2. b)
`2x^2-50=0`
`2x^2=50`
`x^2=25`
`x_1=5`
`x_2=-5`
3.
`3x^2+5x-2=0`
Alkalmazod a megoldóképletet:
`x={-5±sqrt{5^2+4*2*3}}/6={-5±sqrt{25+24}}/6={-5±sqrt49}/6={-5±7}/6`
`x_1={-5+7}/6=2/6=1/3`
`x_2={-5-7}/6=-2`
4.
`4x^4-37x^2+9=0`
Ez az egyenlet x²-re nézve másodfokú.
`x^2={37±sqrt{37^2-4*4*9}}/8={37±sqrt{1369-144}}/8={37±sqrt1225}/8={37±35}/8`
`x_1^2={37+35}/8=9`
`x_2^2={37-35}/8="0,25"`
Még tovább kell folytatni:
`x_1^2=9`
`x_11=3`
`x_12=-3`
`x_2^2="0,25"`
`x_21="0,5"`
`x_22=-"0,5"`
Ezt `x^2=y` helyettesítéssel is megoldhatod.
1
-
máté2009: Nagyon szépen köszönöm. 3 hónapja 0
 AG495
válasza
AG495
válasza
5.
`47-x(3x+4)=2(17-2x)-62`
`109-3x^2-4x=34-4x`
`3x^2=75`
`x^2=25`
`x_1=5`
`x_2=-5`
6.
`x/{2x-1}-1/{2x+1}={x^2+12}/{4x^2-1}`
Felismered, hogy: `4x^2-1=(2x-1)(2x+1)`
Ezzel szorzod az egyenlet minkét oldalát:
`(2x+1)x-(2x-1)=x^2-12`
`2x^2+x-2x+1=x^2-12`
`x^2-x-11=0`
`x={1±sqrt{1+4*11}}/2={1±sqrt45}/2={1±3sqrt5}/2`
`x_1={1+3sqrt5}/2`
`x_2={1-3sqrt5}/2`
Még meg kell nézni, hogy:
`2x-1≠0`
`x≠1/2`
`2x+1≠0`
`x≠-1/2`
`4x^2-1≠0`
Mivel: `4x^2-1=(2x-1)(2x+1)`
Ebből szintén az adódik, hogy: `x≠1/2` és `x≠-1/2`
`x_1` és `x_2` ezektől eltér, vagyis mindkettő megoldása az egyenletnek.
`47-x(3x+4)=2(17-2x)-62`
`109-3x^2-4x=34-4x`
`3x^2=75`
`x^2=25`
`x_1=5`
`x_2=-5`
6.
`x/{2x-1}-1/{2x+1}={x^2+12}/{4x^2-1}`
Felismered, hogy: `4x^2-1=(2x-1)(2x+1)`
Ezzel szorzod az egyenlet minkét oldalát:
`(2x+1)x-(2x-1)=x^2-12`
`2x^2+x-2x+1=x^2-12`
`x^2-x-11=0`
`x={1±sqrt{1+4*11}}/2={1±sqrt45}/2={1±3sqrt5}/2`
`x_1={1+3sqrt5}/2`
`x_2={1-3sqrt5}/2`
Még meg kell nézni, hogy:
`2x-1≠0`
`x≠1/2`
`2x+1≠0`
`x≠-1/2`
`4x^2-1≠0`
Mivel: `4x^2-1=(2x-1)(2x+1)`
Ebből szintén az adódik, hogy: `x≠1/2` és `x≠-1/2`
`x_1` és `x_2` ezektől eltér, vagyis mindkettő megoldása az egyenletnek.
Módosítva: 3 hónapja
1
-
máté2009: Nagyon szépen köszönöm. 3 hónapja 0
 AG495
válasza
AG495
válasza
1.
`y=x^2+8x+15`
Ezt felírhatod így: `y=x^2+8x+16-1`
Itt felismerheted, hogy: `x²+8x+16=(x+4)^2`
Ezek alapján az eredeti függvény felírható így:
`y=(x+4)^2-1`
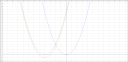
Ez pedig már egyszerűen ábrázolhatod. Az y=x² függvényt eltolod az x tengely mentén negatív irányban négy egységgel, akkor megkapod az y=(x+4)² függvényt. Majd ezt eltolod az y tengely mentén egy egységgel negatív irányban. Ezzel megkapod az y=(x+4)²−1 függvényt, ami megfelel az y=x²+8x+15 függvénynek. Ehhez csatoltam egy rajzot, amelyen a kék az y=x², a piros az y=(x+4)², a zöld az y=(x+4)²−1.
A zérushely ott van, ahol a függvény metszi a x tengelyt. Ezt az x²+8x+15=0 egyenlet megoldásával kapod meg. Az előző példák alapján, remélem ezt már ki tudod számolni. A megoldás x1=−3 és x2=−5. Ezek a zérushelyek. Ez a függvény a zérushelyek középértékénél húzott függőleges egyenesre szimmetrikus és ezen a helyen van a szélső értéke. A zérushelyek középértéke:
`x={-3-5}/2=-4`
Ezt behelyettesítve a függvénybe megkapod a szélsőértéket:
`y=x^2+8x+15=(-4)^2+8*(-4)+15=16-32+15=-1`
A zérushelyeket és a szélsőértéket le is olvashatod a függvény képéről. Már rég tanultam ezeket, ezért nem tudom, hogy a szélsőértéket elég korrektül írtam-e le, ha nem, akkor átfogalmazhatod a mostani tananyag szerint.
`y=x^2+8x+15`
Ezt felírhatod így: `y=x^2+8x+16-1`
Itt felismerheted, hogy: `x²+8x+16=(x+4)^2`
Ezek alapján az eredeti függvény felírható így:
`y=(x+4)^2-1`
Ez pedig már egyszerűen ábrázolhatod. Az y=x² függvényt eltolod az x tengely mentén negatív irányban négy egységgel, akkor megkapod az y=(x+4)² függvényt. Majd ezt eltolod az y tengely mentén egy egységgel negatív irányban. Ezzel megkapod az y=(x+4)²−1 függvényt, ami megfelel az y=x²+8x+15 függvénynek. Ehhez csatoltam egy rajzot, amelyen a kék az y=x², a piros az y=(x+4)², a zöld az y=(x+4)²−1.
A zérushely ott van, ahol a függvény metszi a x tengelyt. Ezt az x²+8x+15=0 egyenlet megoldásával kapod meg. Az előző példák alapján, remélem ezt már ki tudod számolni. A megoldás x1=−3 és x2=−5. Ezek a zérushelyek. Ez a függvény a zérushelyek középértékénél húzott függőleges egyenesre szimmetrikus és ezen a helyen van a szélső értéke. A zérushelyek középértéke:
`x={-3-5}/2=-4`
Ezt behelyettesítve a függvénybe megkapod a szélsőértéket:
`y=x^2+8x+15=(-4)^2+8*(-4)+15=16-32+15=-1`
A zérushelyeket és a szélsőértéket le is olvashatod a függvény képéről. Már rég tanultam ezeket, ezért nem tudom, hogy a szélsőértéket elég korrektül írtam-e le, ha nem, akkor átfogalmazhatod a mostani tananyag szerint.
0
- Még nem érkezett komment!