Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
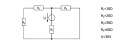
Elektronika hálózatszámítás
 skyrim
kérdése
skyrim
kérdése
486
A feladat az, hogy meg kell határozni az R4 ellenálláson eső feszültséget és rajta átfolyó áram erősségét. Csomóponti potenciálok módszere, hurokáramok módszere, Thevenin- és Norton tétel segítségével külön-külön.
Ahogy elkezdtem:
A CSMP módszernél A-val jelöltem a felső csomópontot, B-vel az alsót, amit földpontnak vettem, VB = 0V-nak.
Az A csomópont feszültsége VA.
Külön kiszámoltam az egyes ellenállásokon átfolyó áramot: I4 = VA/R4, I3 = (VA-U)/R4, I12 = VA/(R1+R2)
Az egyenletet is felírtam, miszerint: I12+I3+I4 = 0, ezekbe behelyettesíttem a fentieket, majd számoltam VA-ra 12V-ot
Innen hogyan tovább? Sajnos elakadtam, és a többihez hozzá sem tudok fogni így...
Ha valaki segítene, és nem feltétlen a kész eredményt adná meg, azt nagyon megköszönném!
Ahogy elkezdtem:
A CSMP módszernél A-val jelöltem a felső csomópontot, B-vel az alsót, amit földpontnak vettem, VB = 0V-nak.
Az A csomópont feszültsége VA.
Külön kiszámoltam az egyes ellenállásokon átfolyó áramot: I4 = VA/R4, I3 = (VA-U)/R4, I12 = VA/(R1+R2)
Az egyenletet is felírtam, miszerint: I12+I3+I4 = 0, ezekbe behelyettesíttem a fentieket, majd számoltam VA-ra 12V-ot
Innen hogyan tovább? Sajnos elakadtam, és a többihez hozzá sem tudok fogni így...
Ha valaki segítene, és nem feltétlen a kész eredményt adná meg, azt nagyon megköszönném!
Jelenleg 1 felhasználó nézi ezt a kérdést.
Elektrónika, áramkörök
Elektrónika, áramkörök
0
Felsőoktatás / Fizika
Válaszok
5 alkst
{ Matematikus }
válasza
alkst
{ Matematikus }
válasza
R1=10 Ohm
R2=20 Ohm
R3=30 Ohm
R4=60 Ohm
U=30 Volt
R1,2=R1+R2=10+20=30 Ohm
R1,2,4=(R1,2 * R4) : (R1,2 + R4) =(30 * 60) : (30 + 60)=20 Ohm
Re=R1,2,4 + R3 = 20+30=50 Ohm
I=I3=I1,2,4=U/Re=30V/50Ohm=0,6 A
U4=U1,2=R1,2,4*I1,2,4=20 Ohm * 0,6 A=12 V
I4=U4/R4=12 V/60 Ohm=0,2 A.
R2=20 Ohm
R3=30 Ohm
R4=60 Ohm
U=30 Volt
R1,2=R1+R2=10+20=30 Ohm
R1,2,4=(R1,2 * R4) : (R1,2 + R4) =(30 * 60) : (30 + 60)=20 Ohm
Re=R1,2,4 + R3 = 20+30=50 Ohm
I=I3=I1,2,4=U/Re=30V/50Ohm=0,6 A
U4=U1,2=R1,2,4*I1,2,4=20 Ohm * 0,6 A=12 V
I4=U4/R4=12 V/60 Ohm=0,2 A.
Módosítva: 5 hónapja
2
-
skyrim: Köszi! 5 hónapja 0
 AG495
válasza
AG495
válasza
I3 az ábra szerint felfelé folyik, így az R3-on eső feszültség is felfelé mutat, UA pedig fentről lefelé, ezért az R3 ellenálláson folyó áram:
I3=(U-UA)/R3
Az A csomópontba befolyik I3 és kifolyik I12 és I4, a csomóponti egyenlet:
I3−I12−I4=0
Egyébként jól számoltál, az UA-ra nekem is 12 V jött ki. Akkor az első kérdésre meg van a válasz:
Az UA az R4 ellenálláson eső feszültség: U4=UA=12 V.
Az R4-en folyó áram: I4=U4/R4=12/60=0,2 A
I3=(U-UA)/R3
Az A csomópontba befolyik I3 és kifolyik I12 és I4, a csomóponti egyenlet:
I3−I12−I4=0
Egyébként jól számoltál, az UA-ra nekem is 12 V jött ki. Akkor az első kérdésre meg van a válasz:
Az UA az R4 ellenálláson eső feszültség: U4=UA=12 V.
Az R4-en folyó áram: I4=U4/R4=12/60=0,2 A
2
- Még nem érkezett komment!
 AG495
válasza
AG495
válasza
A hurokáramok módszerénél kiválasztasz két hurkot. Célszerű (mert így egyszerűbb), ha az egyik a külső hurok, a másik legyen a baloldali hurok. Mindkét hurokban felveszel egy hurokáramot. A baloldali hurokban legyen I1, a külső hurokban legyen I2. Felveszel egy körüljárási irányt, ez legyen az óramutató járásával egyező. A két hurokra felírod a hurokegyenletet.
A külső hurokra: I2·R4+(I1+I2)R12=0
A baloldali hurokra: U+I1·R3+(I1+I2)R12=0
Az első egyenletből kifejezed az I1-et:
I2·R4+I1·R12+I2·R12=0
I1·R12=−I2(R4+R12)
I1=−I2(R4+R12)/R12=−I2(60+30)/30=−3·I2
Ezt behelyettesíted a második egyenletbe: U−3·I2·R3+(−3·I2+I2)R12=0
U−3·I2−2·I2·R12=0
U−I2(3·R3+2·R12)=0
I2=U/(3·R3+2·R12)=30/( 3·30+2·30)=0,2 A
Ez az áram folyik az R4 ellenálláson, a rajta eső feszültség: U4=I2·R4=0,2·60=12 V
A külső hurokra: I2·R4+(I1+I2)R12=0
A baloldali hurokra: U+I1·R3+(I1+I2)R12=0
Az első egyenletből kifejezed az I1-et:
I2·R4+I1·R12+I2·R12=0
I1·R12=−I2(R4+R12)
I1=−I2(R4+R12)/R12=−I2(60+30)/30=−3·I2
Ezt behelyettesíted a második egyenletbe: U−3·I2·R3+(−3·I2+I2)R12=0
U−3·I2−2·I2·R12=0
U−I2(3·R3+2·R12)=0
I2=U/(3·R3+2·R12)=30/( 3·30+2·30)=0,2 A
Ez az áram folyik az R4 ellenálláson, a rajta eső feszültség: U4=I2·R4=0,2·60=12 V
Módosítva: 5 hónapja
2
- Még nem érkezett komment!
 AG495
megoldása
AG495
megoldása
Thevenin tételénél azt az ellenállást, amelyen keresed a feszültséget vagy áramot kiveszed a hálózatból. Meghatározod, hogy így mekkora feszültség van a helyén. Ez lesz a Thevenin helyettesítő feszültséggenerátor üresjárási feszültsége. Majd a hálózatban levő feszültségforrás helyére rövidzárat teszel és meghatározod a kivett ellenállás felől nézve a hálózat eredő ellenállását. Ez lesz a Thevenin helyettesítő feszültséggenerátor belső ellenállása.
Jelen esetben R4-et eltávolítod a hálózatból, a helyén levő feszültség, így az R12-en eső feszültség lesz, amely, mivel R12=R3 a feszültségforrás feszültségének fele:
Uo=U/2=30/2=15 V.
Egyébként meg feszültségosztóval lehetne kiszámolni: Uo=U·R12/(R12+R3)
Az eltávolított R4 helye felől nézve a hálózat ellenállása, úgy, hogy a feszültségforrás helyére rövidzárat képzelünk az R12 és az R3 párhuzamos eredője.
Mivel R12=R3, így: Rb=R12/2=R3/2=30/2=15 Ω.
Így kaptál egy Uo=15 V üresjárási feszültségű, Rb=15 Ω belső ellenállású valóságos feszültséggenerátort, ez a Thevenin helyettesítő feszültséggenerátor. Erre rákapcsolod az R4 ellenállást és kiszámítod a rajta folyó áramot és a rajta eső feszültséget. Eszerint az R4-en folyó áram (Rb és R4 sorosan van kapcsolva): I4=Uo/(Rb+R4)=15/(15+60)=0,2 A
A rajta eső feszültség: U4=I4·R4=0,2·60=12 V
Norton tételénél azt az ellenállást, amelyen keresed a feszültséget vagy áramot, rövidrezárod. Meghatározod, hogy mekkora áram folyik ezen a rövidzáron. Ez lesz a Norton helyettesítő áramgenerátor üresjárási árama. Majd a hálózatban levő feszültségforrás helyére rövidzárat teszel és meghatározod a kivett ellenállás felől nézve a hálózat eredő ellenállását. Ez lesz a Norton helyettesítő áramgenerátor belső ellenállása.
Jelen esetben, ha az R4-et rövidrezárod, azzal egyben rövidrezárod R12-t is. Ezzel a hálózatban csak a feszültségforrás és az R3 marad. A rövidzáron folyó áram:
Io=U/R3=30/30=1 A
Itt arra kell ügyelni, hogy ez az áram az U jelű feszültséggel ellentétes irányú. A belső ellenállása – mivel számítása ugyanúgy történik – megegyezik a Thevenin helyettesítésnél számítottal, Rb=15 Ω. Így kaptál egy Io=1 A üresjárási áramú, Rb=15 Ω belső ellenállású valóságos áramgenerátort, ez a Norton helyettesítő áramgenerátor. Erre rákapcsolod az R4 ellenállást és kiszámítod a rajta folyó áramot és a rajta eső feszültséget. Most Rb és R4 párhuzamosan van kapcsolva, ezért az R4-en folyó áramot az áramosztó képlettel lehet meghatározni:
I4=Io·Rb/(Rb+R4)=1·15/(15+60)=0,2 A
A rajta eső feszültség: U4=I4·R4=0,2·60=12 V
Van még egy egyszerű módszer. Ismeretes, hogy a valóságos feszültséggenerátor átalakítható valóságos áramgenerátorrá. A példánál az ideális feszültséggenerátor és a vele sorosan kapcsolt R3 együtt valóságos feszültséggenerátornak tekinthető. Ez átalakítható valóságos áramgenerátorrá, ennek belső ellenállása megegyezik a valóságos feszültséggenerátor belső ellenállásával, jelen esetben ez Rb=R3=30 Ω. Az üresjárási árama pedig: I=U/Rb=U/R3=30/30=1 A. Itt figyelni kell arra, hogy ez az áram az U feszültséggel ellentétes irányú. Így van egy valóságos áramgenerátor, amelyre párhuzamos kapcsolódik R12 és R4. Végeredményben úgy is tekinthető, hogy van egy ideális áramgenerátor, és erre párhuzamosan kapcsolódnak R3, R12, R4. R12 és R3 párhuzamos eredője R123=30/2=15 Ω, R4=60 Ω. R4-en folyó áram áramosztó képlettel:
I4=I·R123/(R123+R4)=1·15/(15+60)=0,2 A
Jelen esetben R4-et eltávolítod a hálózatból, a helyén levő feszültség, így az R12-en eső feszültség lesz, amely, mivel R12=R3 a feszültségforrás feszültségének fele:
Uo=U/2=30/2=15 V.
Egyébként meg feszültségosztóval lehetne kiszámolni: Uo=U·R12/(R12+R3)
Az eltávolított R4 helye felől nézve a hálózat ellenállása, úgy, hogy a feszültségforrás helyére rövidzárat képzelünk az R12 és az R3 párhuzamos eredője.
Mivel R12=R3, így: Rb=R12/2=R3/2=30/2=15 Ω.
Így kaptál egy Uo=15 V üresjárási feszültségű, Rb=15 Ω belső ellenállású valóságos feszültséggenerátort, ez a Thevenin helyettesítő feszültséggenerátor. Erre rákapcsolod az R4 ellenállást és kiszámítod a rajta folyó áramot és a rajta eső feszültséget. Eszerint az R4-en folyó áram (Rb és R4 sorosan van kapcsolva): I4=Uo/(Rb+R4)=15/(15+60)=0,2 A
A rajta eső feszültség: U4=I4·R4=0,2·60=12 V
Norton tételénél azt az ellenállást, amelyen keresed a feszültséget vagy áramot, rövidrezárod. Meghatározod, hogy mekkora áram folyik ezen a rövidzáron. Ez lesz a Norton helyettesítő áramgenerátor üresjárási árama. Majd a hálózatban levő feszültségforrás helyére rövidzárat teszel és meghatározod a kivett ellenállás felől nézve a hálózat eredő ellenállását. Ez lesz a Norton helyettesítő áramgenerátor belső ellenállása.
Jelen esetben, ha az R4-et rövidrezárod, azzal egyben rövidrezárod R12-t is. Ezzel a hálózatban csak a feszültségforrás és az R3 marad. A rövidzáron folyó áram:
Io=U/R3=30/30=1 A
Itt arra kell ügyelni, hogy ez az áram az U jelű feszültséggel ellentétes irányú. A belső ellenállása – mivel számítása ugyanúgy történik – megegyezik a Thevenin helyettesítésnél számítottal, Rb=15 Ω. Így kaptál egy Io=1 A üresjárási áramú, Rb=15 Ω belső ellenállású valóságos áramgenerátort, ez a Norton helyettesítő áramgenerátor. Erre rákapcsolod az R4 ellenállást és kiszámítod a rajta folyó áramot és a rajta eső feszültséget. Most Rb és R4 párhuzamosan van kapcsolva, ezért az R4-en folyó áramot az áramosztó képlettel lehet meghatározni:
I4=Io·Rb/(Rb+R4)=1·15/(15+60)=0,2 A
A rajta eső feszültség: U4=I4·R4=0,2·60=12 V
Van még egy egyszerű módszer. Ismeretes, hogy a valóságos feszültséggenerátor átalakítható valóságos áramgenerátorrá. A példánál az ideális feszültséggenerátor és a vele sorosan kapcsolt R3 együtt valóságos feszültséggenerátornak tekinthető. Ez átalakítható valóságos áramgenerátorrá, ennek belső ellenállása megegyezik a valóságos feszültséggenerátor belső ellenállásával, jelen esetben ez Rb=R3=30 Ω. Az üresjárási árama pedig: I=U/Rb=U/R3=30/30=1 A. Itt figyelni kell arra, hogy ez az áram az U feszültséggel ellentétes irányú. Így van egy valóságos áramgenerátor, amelyre párhuzamos kapcsolódik R12 és R4. Végeredményben úgy is tekinthető, hogy van egy ideális áramgenerátor, és erre párhuzamosan kapcsolódnak R3, R12, R4. R12 és R3 párhuzamos eredője R123=30/2=15 Ω, R4=60 Ω. R4-en folyó áram áramosztó képlettel:
I4=I·R123/(R123+R4)=1·15/(15+60)=0,2 A
Módosítva: 5 hónapja
2
-
skyrim: Köszönöm a levezetést, és hogy külön magyarázatot is adtál hozzá! Innen már minden világossá vált 5 hónapja 0
 AG495
válasza
AG495
válasza
alkst Kirchhoff tételeivel oldotta meg, én meg a többi módszerrel, így mindegyik megoldást megkaptad. Egyébként, ha nincs megadva, hogy melyik módszert válaszd, akkor – bár ez az adott feladattól is függ – általában Thevenin tételével a legegyszerűbb. A csomóponti feszültségek módszerénél célszerű a hálózatban levő valóságos feszültséggenerátorokat valóságos áramgenerátorokká alakítani. Tulajdonképpen ez volt az utoljára leírt megoldás. Ezzel az UA feszültség igen egyszerűen meghatározható. Ha pedig UA ismert, akkor a többi feszültség és áram már könnyen számítható. A hurokáramok módszerénél célszerű a hálózatban levő valóságos áramgenerátorokat valóságos feszültséggenerátorokká alakítani. Nem kötelező átalakítani, de ezekkel az átalakításokkal egyszerűbben írhatók fel az áramok és feszültségek.
2
- Még nem érkezett komment!