Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
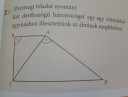
Két derékszögű háromszöget egy-egy oldalukkal egymáshoz illesztettünk az ábrának megfelelően. Így az ABCD derékszögű trapézt kaptuk
Niggerharcos1
kérdése
333
Két derékszögű háromszöget egy-egy oldalukkal egymáshoz illesztettünk az ábrának megfelelően.
Így az ABCD derékszögű trapézt kaptuk.
Legyen AB = 9 cm, AC = 15 cm.
b) Számítsd ki a trapéz kerületét!
c) Számítsd ki a trapéz területét!
Így az ABCD derékszögű trapézt kaptuk.
Legyen AB = 9 cm, AC = 15 cm.
b) Számítsd ki a trapéz kerületét!
c) Számítsd ki a trapéz területét!
Jelenleg 1 felhasználó nézi ezt a kérdést.
Két derékszögű háromszöget egy-egy oldalukkal egymáshoz illesztettünk az ábrának megfelelően. Így az ABCD derékszögű trapézt kaptuk. Legyen AB = 9 cm, AC = 15 cm. b) Számítsd ki a trapéz kerületét! c) Számítsd ki a trapéz területét!
Két derékszögű háromszöget egy-egy oldalukkal egymáshoz illesztettünk az ábrának megfelelően. Így az ABCD derékszögű trapézt kaptuk. Legyen AB = 9 cm, AC = 15 cm. b) Számítsd ki a trapéz kerületét! c) Számítsd ki a trapéz területét!
0
Középiskola / Matematika
Válaszok
1
bazsa990608
{ Közgazdász }
megoldása
Kiszámolod a trapéz derékszöget alkotó oldalát: `"BC"=sqrt("AC"^2-"AB"^2)=sqrt(15^2-9^2)=12 \ "cm"`
Utána ki számolod az `"A"hat"C""B"` szöget: `"A"hat"C""B"=sin^-1 \ "AB"/"AC"=sin^-1 \ 9/15="36,87"°` így meg is tudod határozni az `"A"hat"C""D"` szöget ami: `"A"hat"C""D"=90°-"36,87"°="53,13"°`
Így újabb szögfüggvényekkel kiszámolod a háromszög hiányzó oldalait.
`"CD"="AC"/(cos"A"hat"C""D")=15/(cos"53,13"°)=25 \ "cm"`
`"AD"=sqrt("CD"^2-"AC"^2)=sqrt(25^2-15^2)=20 \ "cm"`
`"K"="AB"+"BC"+"AD"+"CD"=9+12+20+25=color(red)(66 \ "cm")`
`"T"=("AB" \ * \ "BC")/2+("AC" \ * \"AD")/2=(9*12)/2+(15*20)/2=color(red)(204 \ "cm"^2)`
A feladatot fehér színnel oldottam meg amennyiben megoldásnak jelölöd a válaszom elérhetővé teszem számodra a megoldást. Egyéb esetben természetesen nem áll módomban közzétenni. Előre is köszönöm
Utána ki számolod az `"A"hat"C""B"` szöget: `"A"hat"C""B"=sin^-1 \ "AB"/"AC"=sin^-1 \ 9/15="36,87"°` így meg is tudod határozni az `"A"hat"C""D"` szöget ami: `"A"hat"C""D"=90°-"36,87"°="53,13"°`
Így újabb szögfüggvényekkel kiszámolod a háromszög hiányzó oldalait.
`"CD"="AC"/(cos"A"hat"C""D")=15/(cos"53,13"°)=25 \ "cm"`
`"AD"=sqrt("CD"^2-"AC"^2)=sqrt(25^2-15^2)=20 \ "cm"`
`"K"="AB"+"BC"+"AD"+"CD"=9+12+20+25=color(red)(66 \ "cm")`
`"T"=("AB" \ * \ "BC")/2+("AC" \ * \"AD")/2=(9*12)/2+(15*20)/2=color(red)(204 \ "cm"^2)`
A feladatot fehér színnel oldottam meg amennyiben megoldásnak jelölöd a válaszom elérhetővé teszem számodra a megoldást. Egyéb esetben természetesen nem áll módomban közzétenni. Előre is köszönöm
Módosítva: 6 hónapja
1
- Még nem érkezett komment!