Ezt a feladatot most látom 3.jára az oldalon. Mi a probléma vele?

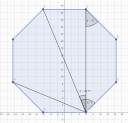
Miért nem megy. Leírom én, hogyan oldanám meg. Behúzod a legrövidebb átlót. Ugye a 8 szög egy belső szöge 135° ez van szembe a legrövidebb átlóval. Ezt a szöget 2 oldal határolja tehát a legrövidebb átlóra felírsz egy coszinusz tételt és kiszámolod és ezzel meg is vagy.

Majd össze kötöd a két szemben lévő átlót így kapsz egy egyenlő szárú trapézt aminek két szöge szintén 135° a másik kettő így értelemszerűen 45°. Behúzod a leghosszabb átlót. Így a szemközti pontokat összekötő egyenes és a leghosszabb átló egy derékszögű háromszöget ad.

A leghosszabb átló másik pontja és a kiindulási pont pontosan felezi a 8 szöget így az egy csúcsban lévő szög a felére csökken azaz 67,5°. Ebből csak ki vonod a 45°-ot és megkapod a derékszögű háromszög egy a befogóval szemközti szögét. Felírsz egy szinusz függvényt az átfogóra és megkaptad a leghosszabb átlót.

Ahogy az ábrán látod úgy.

A beírt kör sugarát kitudod számolni ezzel a képlettel: `r=a/(2*tan \ (180°)/n)`

A köréírható kör sugarát meg kitudod számolni ezzel a képlettel: `R=a/(2sin \ (180°)/n)`

A sugárral már kitudod számolni a körök területét és megnézni az arányukat.

A hasáb térfogatát meg kitudod számolni ezzel a képlettel: `V=(n*a^2*cot \ (180°)/n*m)/4`