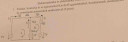Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Elektrotechnika
 zalan2002
kérdése
zalan2002
kérdése
272
Ebben a feladatban szeretném kérni a segítségeteket.
Előre is köszönöm!
Előre is köszönöm!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Fizika
Válaszok
3 AG495
megoldása
AG495
megoldása
Legelőször a sorosan kapcsolt ellenállásokat erdőjükkel helyettesíted:
R1=2+4=6 Ω
R2=5+5=10 Ω
R3=9+3=12 Ω
A feszültséggenerátorok feszültségei:
U1=2 V, U2=3 V, U3=7 V
Kirchhoff törvényeivel:
A fenti csomópontra felírható csomóponti törvény: I1+I2+I3=0
Az I. hurokra felírható huroktörvény: −U1+I1·R1−I2·R2+U2=0
A II. hurokra felírható huroktörvény: −U2+I2·R2−I3·R3+U3=0
Van három egyenlet három ismeretlennel. Az elsőből fejezzük ki I3-mat:
I3=−I1−I2
Ezt helyettesítsük be a harmadik egyenletbe, így marad két egyenlet:
−U1+I1·R1−I2·R2+U2=0
−U2+I2·R2+I1·R3+I2·R3+U3=−U2+I1·R3+I2·(R2+R3)+U3=0
Helyettesítsük be az adatokat:
−2+6·I1−10·I2+3=0
−3+12·I1+22·I2+7=0
1+6·I1−10·I2=0
4+12·I1+22·I2=0
Az első egyenletet szorozzuk meg 2-vel:
2+12·I1−20·I2=0
4+12·I1+22·I2=0
A második egyenletből vonjuk ki az elsőt:
2+42·I2=0
I2=−2/42=1/21≈−0,04762 A=−47,62 mA
I2-re negatív értéket kaptunk, ami azt jelenti, hogy I2 iránya az ábrán jelölttel ellentétes.
Például az 1+6·I1−10·I2=0 egyenletből kifejezzük I1-t:
I1=(10·I2−1)/6=(−10/21−1)/6≈−0,24603 A=−246,03 mA
I1-re is negatív értéket kaptunk, ami azt jelenti, hogy I1 iránya is az ábrán jelölttel ellentétes.
Az I3 áram:
I3=−I1−I2=1/21−(−10/21−1)/6=1/21+(10/21+1)/6≈0,29365 A=293,65 mA
I3 iránya az ábrán jelölttel megegyezik.
R1=2+4=6 Ω
R2=5+5=10 Ω
R3=9+3=12 Ω
A feszültséggenerátorok feszültségei:
U1=2 V, U2=3 V, U3=7 V
Kirchhoff törvényeivel:
A fenti csomópontra felírható csomóponti törvény: I1+I2+I3=0
Az I. hurokra felírható huroktörvény: −U1+I1·R1−I2·R2+U2=0
A II. hurokra felírható huroktörvény: −U2+I2·R2−I3·R3+U3=0
Van három egyenlet három ismeretlennel. Az elsőből fejezzük ki I3-mat:
I3=−I1−I2
Ezt helyettesítsük be a harmadik egyenletbe, így marad két egyenlet:
−U1+I1·R1−I2·R2+U2=0
−U2+I2·R2+I1·R3+I2·R3+U3=−U2+I1·R3+I2·(R2+R3)+U3=0
Helyettesítsük be az adatokat:
−2+6·I1−10·I2+3=0
−3+12·I1+22·I2+7=0
1+6·I1−10·I2=0
4+12·I1+22·I2=0
Az első egyenletet szorozzuk meg 2-vel:
2+12·I1−20·I2=0
4+12·I1+22·I2=0
A második egyenletből vonjuk ki az elsőt:
2+42·I2=0
I2=−2/42=1/21≈−0,04762 A=−47,62 mA
I2-re negatív értéket kaptunk, ami azt jelenti, hogy I2 iránya az ábrán jelölttel ellentétes.
Például az 1+6·I1−10·I2=0 egyenletből kifejezzük I1-t:
I1=(10·I2−1)/6=(−10/21−1)/6≈−0,24603 A=−246,03 mA
I1-re is negatív értéket kaptunk, ami azt jelenti, hogy I1 iránya is az ábrán jelölttel ellentétes.
Az I3 áram:
I3=−I1−I2=1/21−(−10/21−1)/6=1/21+(10/21+1)/6≈0,29365 A=293,65 mA
I3 iránya az ábrán jelölttel megegyezik.
1
- Még nem érkezett komment!
 AG495
válasza
AG495
válasza
Az előző jelölésekkel:
R1=2+4=6 Ω
R2=5+5=10 Ω
R3=9+3=12 Ω
A feszültséggenerátorok feszültségei:
U1=2 V, U2=3 V, U3=7 V
Hurokáramok módszerével:
Az ábrán jelölt két hurokban felveszel egy-egy áramot, célszerűen az I. hurokban I1-gyel jelölhető, a II. hurokban I3-mal. Ezekkel felírod a két hurokra a hurok egyenleteket:
−U1+I1·R1+(I1−I3)·R2+U2=0
−U2+(I3−I1)·R2+I3·R3+U3=0
Az első egyenletben R2 szorzója azért I1−I3, mert az I. hurokban I3 iránya a felvett iránnyal ellentétes, I1 iránya pedig megegyezik azzal. A második egyenletben R2 szorzója azért I3−I1, mert a II. hurokban I1 iránya ellentétes a felvett iránnyal I3 iránya megegyezik azzal. Két egyenlet van két ismeretlennel. Kissé átrendezve:
−U1+I1·(R1+R2)−I3·R2+U2=0
−U2−I1·R2+I3·(R2+R3)+U3=0
Az adatokat behelyettesítve:
−2+16·I1−10·I3+3=0
−3−10·I1+22·I3+7=0
1+16·I1−10·I3=0
4−10·I1+22·I3=0
Az első egyenletet szorozzuk meg 2,2-vel:
2,2+35,2·I1−22·I3=0
4−10·I1+22·I3=0
Adjuk össze a két egyenletet:
6,2+25,2·I1=0
I1=−6,2/25,2≈0,24603 A=−246,03 mA
Az 1+16·I1−10·I3=0 egyenletből kifejezve I3-mat:
I3=(1+16·I1)/10=(1−16·0,24603)/1≈−0,29365 A=−293,65 mA
I1 és I3 negatív lett, ez azt jelenti, hogy a valóságos irányuk a felvett hurokirányokkal ellentétes. Az I2 áram:
I2=I3−I1=293,65−246,03=47,62 mA
Valóságos iránya az ábrán jelölttel ellentétes, vagyis felfelé mutat.
R1=2+4=6 Ω
R2=5+5=10 Ω
R3=9+3=12 Ω
A feszültséggenerátorok feszültségei:
U1=2 V, U2=3 V, U3=7 V
Hurokáramok módszerével:
Az ábrán jelölt két hurokban felveszel egy-egy áramot, célszerűen az I. hurokban I1-gyel jelölhető, a II. hurokban I3-mal. Ezekkel felírod a két hurokra a hurok egyenleteket:
−U1+I1·R1+(I1−I3)·R2+U2=0
−U2+(I3−I1)·R2+I3·R3+U3=0
Az első egyenletben R2 szorzója azért I1−I3, mert az I. hurokban I3 iránya a felvett iránnyal ellentétes, I1 iránya pedig megegyezik azzal. A második egyenletben R2 szorzója azért I3−I1, mert a II. hurokban I1 iránya ellentétes a felvett iránnyal I3 iránya megegyezik azzal. Két egyenlet van két ismeretlennel. Kissé átrendezve:
−U1+I1·(R1+R2)−I3·R2+U2=0
−U2−I1·R2+I3·(R2+R3)+U3=0
Az adatokat behelyettesítve:
−2+16·I1−10·I3+3=0
−3−10·I1+22·I3+7=0
1+16·I1−10·I3=0
4−10·I1+22·I3=0
Az első egyenletet szorozzuk meg 2,2-vel:
2,2+35,2·I1−22·I3=0
4−10·I1+22·I3=0
Adjuk össze a két egyenletet:
6,2+25,2·I1=0
I1=−6,2/25,2≈0,24603 A=−246,03 mA
Az 1+16·I1−10·I3=0 egyenletből kifejezve I3-mat:
I3=(1+16·I1)/10=(1−16·0,24603)/1≈−0,29365 A=−293,65 mA
I1 és I3 negatív lett, ez azt jelenti, hogy a valóságos irányuk a felvett hurokirányokkal ellentétes. Az I2 áram:
I2=I3−I1=293,65−246,03=47,62 mA
Valóságos iránya az ábrán jelölttel ellentétes, vagyis felfelé mutat.
Módosítva: 1 éve
2
- Még nem érkezett komment!
 AG495
válasza
AG495
válasza
Az előző jelölésekkel:
R1=2+4=6 Ω
R2=5+5=10 Ω
R3=9+3=12 Ω
A feszültséggenerátorok feszültségei:
U1=2 V, U2=3 V, U3=7 V
Csomóponti feszültségek módszerével:
Ehhez a valóságos feszültséggenerátorokat valóságos áramgenerátorokká kell alakítani. Mindegyik ideális feszültséggenerátorral sorosan van kapcsolva két (de a fentiek szerint ezeket már összevontuk eggyé) ellenállás. Az ideális feszültséggenerátor és ezek az ellenállások együtt valóságos feszültséggenerátoroknak tekinthetők. Ezek: U1 és R1, U2 és R2, U3 és R3. Az ezek átalakításával létrejött valóságos áramgenerátorok áramai mind az ábra szerint felfelé mutatnak, a feszültséggenerátorok feszültségével ellentétes irányba. Ezek az áramok az ideális feszültséggenerátorok feszültségei és a velük sorosan kapcsolt ellenállások (mint belső ellenállások) hányadosai. Az egyes valóságos áramgenerátorok üresjárási áramai:
I01=U1/R1=2/6=1/3≈0,333 A
I02=U2/R2=3/10=0,3 A
I03=U3/R3=7/12≈0,583 A
Így lesz három párhuzamosan kapcsolt valóságos áramgenerátor. Tulajdonképpen van három párhuzamosan kapcsolt ideális áramgenerátor és ezekkel párhuzamosan van kapcsolva R1, R2 és R3. A három párhuzamosan kapcsolt ideális áramgenerátor árama összeadódik:
I0=I01+I02+I03=1/3+0,3+7/12=1,217 A
Ez az áram a párhuzamos kapcsolt R1, R2, R3 ellenállásokon átfolyva azokon feszültséget ejt.
R1, R2, R3 párhuzamos eredője:
Re=1/(1/R1+1/R2+1/R3)=1/(1/6+1/10+1/12)=12/(2+1,2+1)=12/4,2≈2,857 Ω
Re ellenálláson eső feszültség:
Ue=I0·Re=1,217·2,857=3,476 V
Ez a feszültség a két csomópont közötti feszültség, iránya a rajz szerint fentről lefelé mutat. Most vissza kell térni az eredeti hálózatba. Miután a két csomópont közötti feszültség ismert az egyes áramok számítása igen egyszerű:
I1=(Ue−U1)/R1=(3,476−2)/6=0,246 A=246 mA
I2=(Ue−U2)/R2=(3,476−3)/10=0,0476 A=47,6 mA
I3=(U3−Ue)/R1=(7−3,476)/12=0,29367 A=293,67 mA
Az egyes módszerek eredményei közötti kismértékű eltérés a kerekítések miatt van.
R1=2+4=6 Ω
R2=5+5=10 Ω
R3=9+3=12 Ω
A feszültséggenerátorok feszültségei:
U1=2 V, U2=3 V, U3=7 V
Csomóponti feszültségek módszerével:
Ehhez a valóságos feszültséggenerátorokat valóságos áramgenerátorokká kell alakítani. Mindegyik ideális feszültséggenerátorral sorosan van kapcsolva két (de a fentiek szerint ezeket már összevontuk eggyé) ellenállás. Az ideális feszültséggenerátor és ezek az ellenállások együtt valóságos feszültséggenerátoroknak tekinthetők. Ezek: U1 és R1, U2 és R2, U3 és R3. Az ezek átalakításával létrejött valóságos áramgenerátorok áramai mind az ábra szerint felfelé mutatnak, a feszültséggenerátorok feszültségével ellentétes irányba. Ezek az áramok az ideális feszültséggenerátorok feszültségei és a velük sorosan kapcsolt ellenállások (mint belső ellenállások) hányadosai. Az egyes valóságos áramgenerátorok üresjárási áramai:
I01=U1/R1=2/6=1/3≈0,333 A
I02=U2/R2=3/10=0,3 A
I03=U3/R3=7/12≈0,583 A
Így lesz három párhuzamosan kapcsolt valóságos áramgenerátor. Tulajdonképpen van három párhuzamosan kapcsolt ideális áramgenerátor és ezekkel párhuzamosan van kapcsolva R1, R2 és R3. A három párhuzamosan kapcsolt ideális áramgenerátor árama összeadódik:
I0=I01+I02+I03=1/3+0,3+7/12=1,217 A
Ez az áram a párhuzamos kapcsolt R1, R2, R3 ellenállásokon átfolyva azokon feszültséget ejt.
R1, R2, R3 párhuzamos eredője:
Re=1/(1/R1+1/R2+1/R3)=1/(1/6+1/10+1/12)=12/(2+1,2+1)=12/4,2≈2,857 Ω
Re ellenálláson eső feszültség:
Ue=I0·Re=1,217·2,857=3,476 V
Ez a feszültség a két csomópont közötti feszültség, iránya a rajz szerint fentről lefelé mutat. Most vissza kell térni az eredeti hálózatba. Miután a két csomópont közötti feszültség ismert az egyes áramok számítása igen egyszerű:
I1=(Ue−U1)/R1=(3,476−2)/6=0,246 A=246 mA
I2=(Ue−U2)/R2=(3,476−3)/10=0,0476 A=47,6 mA
I3=(U3−Ue)/R1=(7−3,476)/12=0,29367 A=293,67 mA
Az egyes módszerek eredményei közötti kismértékű eltérés a kerekítések miatt van.
2
- Még nem érkezett komment!