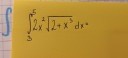Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Ezt hogyan lehet kiszámolni?
 blue
kérdése
blue
kérdése
279
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 bazsa990608
{ Közgazdász }
megoldása
bazsa990608
{ Közgazdász }
megoldása
`int_3^5 \ 2x^2sqrt(2+x^3)dx`
Vezessünk be egy ismeretlent a gyök alatti tényezőre. Legyen pl.: `u`
`u=2+x^3=>du=3x^2dx`
Ebből következik, hogy: `x^2 \ dx=1/3 \ du`
Ennek hatására a határok az alább módon változnak:
- Ha `x=3` akkor `u=2+3^3=29`
- ha `x=5` akkor `u=2+5^3=127`
Így az integrál átalakul:
`int_3^5 \ 2x^2sqrt(2+x^3)dx=int_29^127 \ 2*1/3sqrtu \ du=2/3int_29^127sqrtu \ du`
Most használjuk ki az `intsqrtu \ du=int \ u^(1/2) \ du` primitív függvényét:
`int \ u^(1/2) \ du=u^(3/2)/(3/2)=2/3u^(3/2)`
Így az integrál: `2/3int_29^127sqrtu \ du=2/3*[2/3u^(3/2)]_29^127=4/9*[127^(3/2)-29^(3/2)]=color(red)("566,69")`
A feladatot fehér színnel oldottam meg amennyiben megoldásnak jelölöd a válaszom elérhetővé teszem számodra a megoldást. Egyéb esetben természetesen nem áll módomban közzétenni. Előre is köszönöm
Vezessünk be egy ismeretlent a gyök alatti tényezőre. Legyen pl.: `u`
`u=2+x^3=>du=3x^2dx`
Ebből következik, hogy: `x^2 \ dx=1/3 \ du`
Ennek hatására a határok az alább módon változnak:
- Ha `x=3` akkor `u=2+3^3=29`
- ha `x=5` akkor `u=2+5^3=127`
Így az integrál átalakul:
`int_3^5 \ 2x^2sqrt(2+x^3)dx=int_29^127 \ 2*1/3sqrtu \ du=2/3int_29^127sqrtu \ du`
Most használjuk ki az `intsqrtu \ du=int \ u^(1/2) \ du` primitív függvényét:
`int \ u^(1/2) \ du=u^(3/2)/(3/2)=2/3u^(3/2)`
Így az integrál: `2/3int_29^127sqrtu \ du=2/3*[2/3u^(3/2)]_29^127=4/9*[127^(3/2)-29^(3/2)]=color(red)("566,69")`
A feladatot fehér színnel oldottam meg amennyiben megoldásnak jelölöd a válaszom elérhetővé teszem számodra a megoldást. Egyéb esetben természetesen nem áll módomban közzétenni. Előre is köszönöm

Módosítva: 1 éve
2
- Még nem érkezett komment!