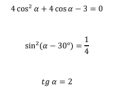Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek házi
 daviid242
kérdése
daviid242
kérdése
252
Sziasztok, ennek a három feladatnak a megoldasahoz kene segitség ugy hogy fokokban legyen szamolva
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 bazsa990608
{ Közgazdász }
megoldása
bazsa990608
{ Közgazdász }
megoldása
1.)
`4cos^2alpha+4cosalpha-3=0`
Bevezetünk egy új ismeretlent, hogy könnyebben tudjunk számolni. Majd megoldjuk a másodfokú egyenletet.
`cos^2alpha=t^2`
`cosalpha=t`
`4t^2+4t-3=0`
`t_(1,2) = (-b+-sqrt(b^2-4ac))/(2a)=(-4+-sqrt(4^2-4*4*(-3)))/(2*4)={(t_1=1/2) , (cancel(t_2 ="-"3/2)):}`
`cosalpha_1=1/2=>alpha_1=60°`
`cosalpha_2=360°-cosalpha_1=>alpha_2=360°-60°=alpha_2=300°`
A megoldást az uniók meghatározás után kapjuk:
- `color(red)(alpha=60°+360°k, k in ZZ)`
- `color(red)(alpha=300°+360°k, k in ZZ)`
2.)
`sin^2(alpha-30°)=1/4`
`sin^2(alpha-30°)=+-1/2`
Ebből két lehetőség is adódik:
- Ebből az első:
`sin(alpha-30°)="-"1/2`
`alpha-30°=210°`
`alpha=240°`
- A második:
`sin(alpha-30°)="-"1/2`
`alpha-30°=330°`
`alpha=360°`
`sin^2(alpha-30°)=1/2`
`sinalpha-30°=30°`
`alpha=60°`
`sin^2(alpha-30°)=1/2`
`alpha-30°=150°`
`alpha=180°`
A megoldást az uniók meghatározás után kapjuk:
- `color(red)(alpha=180°k, k in ZZ)`
-`color(red)(alpha=60°k,+180° k in ZZ)`
3.)
`tgalpha=2`
`alpha=tg^-1 \ 2`
`alpha="63,4"°`
Megoldás: `color(red)(alpha="63,4"°+180°k;k in ZZ)`
A feladatot fehér színnel oldottam meg amennyiben megoldásnak jelölöd a válaszom elérhetővé teszem számodra a megoldást. Egyéb esetben természetesen nem áll módomban közzétenni. Előre is köszönöm
`4cos^2alpha+4cosalpha-3=0`
Bevezetünk egy új ismeretlent, hogy könnyebben tudjunk számolni. Majd megoldjuk a másodfokú egyenletet.
`cos^2alpha=t^2`
`cosalpha=t`
`4t^2+4t-3=0`
`t_(1,2) = (-b+-sqrt(b^2-4ac))/(2a)=(-4+-sqrt(4^2-4*4*(-3)))/(2*4)={(t_1=1/2) , (cancel(t_2 ="-"3/2)):}`
`cosalpha_1=1/2=>alpha_1=60°`
`cosalpha_2=360°-cosalpha_1=>alpha_2=360°-60°=alpha_2=300°`
A megoldást az uniók meghatározás után kapjuk:
- `color(red)(alpha=60°+360°k, k in ZZ)`
- `color(red)(alpha=300°+360°k, k in ZZ)`
2.)
`sin^2(alpha-30°)=1/4`
`sin^2(alpha-30°)=+-1/2`
Ebből két lehetőség is adódik:
- Ebből az első:
`sin(alpha-30°)="-"1/2`
`alpha-30°=210°`
`alpha=240°`
- A második:
`sin(alpha-30°)="-"1/2`
`alpha-30°=330°`
`alpha=360°`
`sin^2(alpha-30°)=1/2`
`sinalpha-30°=30°`
`alpha=60°`
`sin^2(alpha-30°)=1/2`
`alpha-30°=150°`
`alpha=180°`
A megoldást az uniók meghatározás után kapjuk:
- `color(red)(alpha=180°k, k in ZZ)`
-`color(red)(alpha=60°k,+180° k in ZZ)`
3.)
`tgalpha=2`
`alpha=tg^-1 \ 2`
`alpha="63,4"°`
Megoldás: `color(red)(alpha="63,4"°+180°k;k in ZZ)`
A feladatot fehér színnel oldottam meg amennyiben megoldásnak jelölöd a válaszom elérhetővé teszem számodra a megoldást. Egyéb esetben természetesen nem áll módomban közzétenni. Előre is köszönöm

Módosítva: 1 éve
2
-
daviid242: Szia, megjelöltem. 1 éve 0