Az egyetlen érdekes kérdés a henger alakú doboz alapjának a sugara. Ez 2 részből tevődik össze:
    • gyertya középpontja és a doboz középpontja közti távolság: `sqrt(3^2 + 3^2) = 4.242641 cm`
    • gyertya középpontja és a doboz oldala közti távolság: `3 cm`
Összesen tehát `4.242641 + 3 = 7.242641 cm`

Ezután csak kiszámítjuk ami kezünk ügyébe kerül:
`K_t = 2 * a + 2 * b = 2 * 24 + 2 + 6 = 60 cm`
`K_n = 4 * a = 4 * 12 = 48 cm`
`K_k = 2 * r * \pi = 2 * 7.242641 * \pi = 45.506854 cm`

`T_t = a * b = 24 * 6 = 144 cm^2`
`T_n = a^2 = 12^2 = 144 cm^2`
`T_k = r^2 * \pi = 7.242641^2 * \pi = 164.794895 cm^2`

`F_t = T_t * 2 + K_t *9 = 144 * 2 + 60 * 9 = 828 cm^2`
`F_n = T_n * 2 + K_n * 9 = 144 * 2 + 48 * 9 = 720 cm^2`
`F_k = T_k * 2 + F_k * 9 = 164.794895 * 2 + 45.506854 * 9 = 739.151471 cm^2`

`V_t = T_t * m = 144 * 9 = 1296 cm^3`
`V_n = T_n * 9 = 144 * 9 = 1296 cm^3`
`V_k = T_k * 9 = 164.794895 * 9 = 1483.154051 cm^3`

`V_{gy} = r^2 * \pi * m = 3^2 * \pi * 9 = 254.469005 cm^3`
`V_á = 4 * V_{gy} = 1017.876020 cm^3`

És máris meg tudjuk válaszolni a kérdéseket:

a) A legkisebb a `F_t`, `F_n` és `F_k` közül, tehát a négyzet alapú dobozhoz kell a legkevesebb karton.

b) A doboz térfogata a gyertyák térfogatának `V_{doboz} * 100 // V_{árú}` százaléka:
    • téglalap és négyzet: `1296 * 100 // 1017.876020 = 127.323955 %`
    • kör: `1483.154051 * 100 // 1017.876020 = 145.710678 %`

c) A doboz térfogatának `(V_{doboz} - V_{árú}) * 100 // V_{doboz}` százaléka üres:
    • téglalap és négyzet: `(1296 - 1017.876020) * 100 // 1296 = 21.460184 %`
    • kör: `(1483.154051 - 1017.876020) * 100 // 1483.154051 = 31.370850 %`

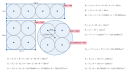
Ellenőrzésként lásd az ábrán a GeoGebra számításait rózsaszín alapon.

a)
Ahhoz, hogy összehasonlítsuk az anyagfelhasználást mindhárom esetre meg kell határozni a doboz felszínét.
1. Négy gyertya egymás mellett elhelyezve.
A doboz ekkor téglatest alakú, melynek magassága egyenlő a gyertyák magasságával (m=9 cm), az alap hosszabb oldaléle a=4d=4·6=24 cm, a rövidebb oldaléle b=d=6 cm.
A felület: A1=2(ab+am+bm)=2·(24·6+24·9+6·9)=828 cm²
2. Négy gyertya négyzet alapú dobozban elhelyezve.
A doboz magassága most is egyenlő a gyertyák magasságával (m=9 cm), alapja pedig négyzet, melynek oldalélei a=2d=2·6=12 cm
A felület: A2=2a²+4am=2a(a+2m)=2·12·(12+2·9)=720 cm²
3. Négy gyertya kör alapú dobozban elhelyezve.
A doboz most henger alakú, magassága m=9 cm, ismerni kell a doboz alapjának sugarát, ez:
R=r+√ 2 r=r(1+√ 2 )=3·(1+√ 2 )=7,243 cm
A csatolt rajzon láthatod miért ennyi.
A felület: A3=2R²π+2Rπm=2Rπ(R+m)=2·7,243·π·(7,243+9)=739,2 cm²
Ezek alapján a 2. esetben a legkisebb a doboz anyagszükséglete.
b)
Négy gyertya térfogata együttesen:
Vgy=4·r²·π·m=4·3²·π·9=1017,88 cm³
Az 1. esetben a doboz térfogata:
V1=a·b·m=24·6·9=1296 cm³
A 2. esetben a doboz térfogata:
V2=a²·m=12²·9=1296 cm³
A 3. esetben a doboz térfogata:
V3=R²·π·m=7,243²·π·9=1483,3 cm³
A dobozok térfogata a gyertyák együttes térfogatához képest százalékban:
1. 100·V1/Vg=100·1296/1017,88=127,32%
2. 100·V2/Vg=100·1296/1017,88=127,32%
3. 100·V3/Vg=100·1483,3/1017,88=145,72%
c)
A doboz térfogatának hány százaléka üres? Ehhez a doboz térfogatából le kell vonni a négy gyertya együttes térfogatát, majd ez arányítani kell a doboz térfogatához.
1. 100·(V1−Vgy)/V1=100·(1−Vgy/V1)=100·(1−1017,88/1296)=21,46%
2. 100·(1−Vgy/V2)=100·(1−1017,88/1296)=21,46%
3. 100·(1−Vgy/V3)=100·(1−1017,88/1483,3)=31,38%