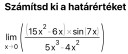Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Számitsd ki a határértéket
 nemeslace1919
kérdése
nemeslace1919
kérdése
335
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
matek, határérték
matek, határérték
0
Felsőoktatás / Matematika
Válaszok
2 bazsa990608
{ Közgazdász }
megoldása
bazsa990608
{ Közgazdász }
megoldása
Ahogy látom leminuszoltad a válaszom ami azt jelenti hogy szerinted a válasz rossz pedig még nem is láttad, ez esetben be se írom várj csak nyugodtan tovább órákat. Majd legközelebb tanulsz egy kis türelmet.  szép napot.
szép napot.
A feladatot fehér színnel oldottam meg amennyiben megoldásnak jelölöd a válaszom elérhetővé teszem számodra a megoldást. Egyéb esetben természetesen nem áll módomban közzétenni. Előre is köszönöm
 szép napot.
szép napot.A feladatot fehér színnel oldottam meg amennyiben megoldásnak jelölöd a válaszom elérhetővé teszem számodra a megoldást. Egyéb esetben természetesen nem áll módomban közzétenni. Előre is köszönöm

Módosítva: 1 éve
-1
- Még nem érkezett komment!
 kazah
válasza
kazah
válasza
= `lim_(x to 0) (3*cancel(x)*(5x-2)*sin(7x))/(x^(cancel(2))*(5x-4)` =
Az `(5x-2)/(5x-4)` határértéke, ha x tart a nullához (behelyettesíted) `(5*0-2)/(5*0-4)` = `(-2)/(-4)` = `1/2`
`lim_(x to 0) (3*7*sin(7x))/(2*7*x)` = `(21*1)/2` = `21/2`
A `lim_(x to 0) (sinx)/x` = 1 összefüggést gondolom ismert, a 7x ne zavarjon, kibővítettük, mondjuk `7x = a` esetre lesz `lim_(a to 0) (sina)/a` = 1.
A megoldás tehát `21/2`.
Az `(5x-2)/(5x-4)` határértéke, ha x tart a nullához (behelyettesíted) `(5*0-2)/(5*0-4)` = `(-2)/(-4)` = `1/2`
`lim_(x to 0) (3*7*sin(7x))/(2*7*x)` = `(21*1)/2` = `21/2`
A `lim_(x to 0) (sinx)/x` = 1 összefüggést gondolom ismert, a 7x ne zavarjon, kibővítettük, mondjuk `7x = a` esetre lesz `lim_(a to 0) (sina)/a` = 1.
A megoldás tehát `21/2`.
3
- Még nem érkezett komment!