Keresés


Toplista

Toplista
  • betöltés...

Magántanár kereső

Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!

Matematika

Főoldal » Általános iskola » Matematika
316
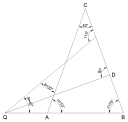
Kérlek segítsetek!
Matematika – feladat kép 1
Matematika – feladat kép 2
Matematika – feladat kép 3
Matematika – feladat kép 4
Matematika – feladat kép 5
Jelenleg 1 felhasználó nézi ezt a kérdést.
szöveges
0
Általános iskola / Matematika

Válaszok

1
5.
ABC egyenlő szárú háromszög, szárszöge 40°. A másik két szöge:
α=ε=(180°−40°)/2=70°
δ=180°−110°−40°=30°
β=180°−(180°−70°)−30°=40°
Csatolok hozzá egy arányos ábrát:
Matematika – megoldás kép 1
2