Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Elektromos áramkörök IV.
 Vicu
{ Elismert } kérdése
Vicu
{ Elismert } kérdése
257
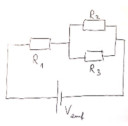
Határozza meg az R1, R2 és R3 egyes ellenállások P1, P2 és P3 teljesítményfogyasztását.
R1=360 ohm
R2=1,2 k.ohm
R3=800 ohm
Elektromotoros erő V emf=28 V
R1=360 ohm
R2=1,2 k.ohm
R3=800 ohm
Elektromotoros erő V emf=28 V
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Fizika
Válaszok
1 vikoca3456
megoldása
vikoca3456
megoldása
Megoldás
Elektromos áramkör teljesítményfogyasztásának kiszámítása
1) A feladat összefoglalása és az adatok:
Adott egy elektromos áramkör, amelyben három ellenállás (R1, R2, R3) található. Az egyes ellenállások értéke ismert:
R1 = 360 ohm
R2 = 1,2 k.ohm = 1200 ohm (1 k.ohm = 1000 ohm)
R3 = 800 ohm
Az áramkör elektromotoros ereje (feszültsége) is ismert:
V_emf = 28 V
Meg kell határoznunk az egyes ellenállásokon (P1, P2, P3) eső teljesítményfogyasztást.
2) A cél:
A célunk az egyes ellenállások teljesítményfogyasztásának (P1, P2, P3) kiszámítása.
3) A megoldás terve:
Az egyes ellenállásokon átfolyó áram (I1, I2, I3) kiszámítása: Ehhez felhasználjuk az Ohm-törvényt (V = I * R) és az áramkör soros és párhuzamos kapcsolásának szabályait.
Az egyes ellenállásokon eső teljesítmény (P1, P2, P3) kiszámítása: Ehhez a P = I^2 * R vagy a P = V^2 / R képletet használjuk, ahol a megfelelő áramokat és feszültségeket alkalmazzuk.
4) A megoldás lépésről lépésre:
4.1) Az R2 és R3 eredő ellenállásának kiszámítása (R23):
R2 és R3 párhuzamosan vannak kapcsolva, ezért az eredő ellenállásukat a következőképpen számolhatjuk ki:
1/R23 = 1/R2 + 1/R3
1/R23 = 1/1200 + 1/800
1/R23 = 5/2400
R23 = 2400/5 = 480 ohm
Az R2 és R3 ellenállások eredő ellenállása (R23) tehát 480 ohm.
4.2) Az áramkör eredő ellenállásának kiszámítása (Re):
Az R23 eredő ellenállás sorba van kapcsolva R1-el, így az áramkör eredő ellenállása (Re):
Re = R1 + R23
Re = 360 ohm + 480 ohm
Re = 840 ohm
Az áramkör eredő ellenállása (Re) tehát 840 ohm.
4.3) Az áramkörben folyó áram (I) kiszámítása:
Az áramkörben folyó áram (I) kiszámításához az Ohm-törvényt használjuk:
V = I * R
I = V / R
I = 28 V / 840 ohm
I = 0.0333 A = 33.3 mA
Az áramkörben 33.3 mA áram folyik.
4.4) Az R1 ellenálláson átfolyó áram (I1) kiszámítása:
Mivel R1 sorba van kapcsolva az R23 eredő ellenállással, ezért az R1-en átfolyó áram (I1) megegyezik az áramkörben folyó árammal (I):
I1 = I = 33.3 mA
Az R1 ellenálláson 33.3 mA áram folyik.
4.5) Az R2 és R3 ellenállásokon átfolyó áram (I2, I3) kiszámítása:
Mivel R2 és R3 párhuzamosan vannak kapcsolva, ezért az áram elágazik rajtuk. Az egyes ellenállásokon átfolyó áramot az áramosztás szabálya alapján számolhatjuk ki:
I2 = I * (R3 / (R2 + R3))
I2 = 33.3 mA * (800 ohm / (1200 ohm + 800 ohm))
I2 = 13.3 mA
I3 = I * (R2 / (R2 + R3))
I3 = 33.3 mA * (1200 ohm / (1200 ohm + 800 ohm))
I3 = 20 mA
Az R2 ellenálláson 13.3 mA, az R3 ellenálláson pedig 20 mA áram folyik.
4.6) Az egyes ellenállásokon eső teljesítmény (P1, P2, P3) kiszámítása:
Az egyes ellenállásokon eső teljesítményt a P = I^2 * R képlettel számolhatjuk ki:
P1 = I1^2 * R1
P1 = (0.0333 A)^2 * 360 ohm
P1 = 0.4 W
P2 = I2^2 * R2
P2 = (0.0133 A)^2 * 1200 ohm
P2 = 0.21 W
P3 = I3^2 * R3
P3 = (0.02 A)^2 * 800 ohm
P3 = 0.32 W
Tehát az egyes ellenállásokon eső teljesítményfogyasztás:
P1 = 0.4 W
P2 = 0.21 W
P3 = 0.32 W
5) Ellenőrzés:
Ellenőrizhetjük a számításainkat, ha összeadjuk az egyes ellenállásokon eső teljesítményfogyasztást, és megnézzük, hogy megegyezik-e a teljesítményfogyasztással (P_total):
P_total = V_emf * I
P_total = 28 V * 0.0333 A
P_total = 0.93 W
P1 + P2 + P3 = 0.4 W + 0.21 W + 0.32 W = 0.93 W
Mivel P_total = P1 + P2 + P3, a számításaink helyesek
2
- Még nem érkezett komment!