Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Elektromos áramkörök III.
 Vicu
{ Elismert } kérdése
Vicu
{ Elismert } kérdése
244
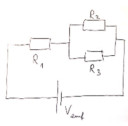
Határozza meg az R1, R2 és R3 egyes ellenállásokon átívelő V1, V2 és V3 feszültségeket!
R1=360 ohm
R2=1,2 k.ohm
R3=800 ohm
Elektromotoros erő V emf=28 V
R1=360 ohm
R2=1,2 k.ohm
R3=800 ohm
Elektromotoros erő V emf=28 V
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Fizika
Válaszok
1 vikoca3456
megoldása
vikoca3456
megoldása
Megoldás
Elektromos áramkör feladat megoldása
1. A feladat összefoglalása és az adatok:
Adott egy elektromos áramkör, amelyben három ellenállás (R1, R2, R3) található. Az áramkört egy V_emf elektromotoros erejű feszültségforrás táli.
Ismert adatok:
R1 = 360 ohm
R2 = 1,2 kΩ = 1200 ohm (mivel 1 kΩ = 1000 ohm)
R3 = 800 ohm
V_emf = 28 V
2. A feladat célja:
Ki kell számolni az egyes ellenállásokon (R1, R2, R3) eső feszültségeket (V1, V2, V3).
3. A megoldás terve:
Kiszámoljuk az áramkör eredő ellenállását (R_eredő).
Kiszámoljuk az áramkörben folyó áram erősségét (I).
Ohm törvénye alapján kiszámoljuk az egyes ellenállásokon eső feszültségeket (V1, V2, V3).
4. A feladat megoldása lépésről lépésre:
a) Az eredő ellenállás (R_eredő) kiszámítása:
R2 és R3 párhuzamosan vannak kapcsolva. A párhuzamosan kapcsolt ellenállások eredő ellenállásának reciproka egyenlő az egyes ellenállások reciprokának összegével:
1/R23 = 1/R2 + 1/R3
1/R23 = 1/1200 + 1/800 = 5/2400
Ebből R23 = 2400/5 = 480 ohm
Az R23 eredő ellenállás sorosan van kapcsolva R1-el. A sorosan kapcsolt ellenállások eredő ellenállása egyenlő az egyes ellenállások összegével:
R_eredő = R1 + R23
R_eredő = 360 + 480 = 840 ohm
b) Az áramkörben folyó áram (I) kiszámítása:
Ohm törvénye szerint az áram erőssége (I) egyenlő a feszültség (V) és az ellenállás (R) hányadosával:
I = V_emf / R_eredő
I = 28 V / 840 ohm = 0.0333 A = 33.3 mA
c) Az egyes ellenállásokon eső feszültségek (V1, V2, V3) kiszámítása:
V1 = I * R1 (Ohm törvénye)
V1 = 0.0333 A * 360 ohm = 12 V
V2 = V3 = I * R23 (párhuzamos kapcsolás miatt a feszültség egyforma)
V2 = V3 = 0.0333 A * 480 ohm = 16 V
5. Ellenőrzés:
A Kirchhoff feszültségi törvénye szerint a zárt áramkörben a feszültségesések összege egyenlő a feszültségforrás elektromotoros erejével:
V_emf = V1 + V2
28 V = 12 V + 16 V
28 V = 28 V
Az egyenlet teljesül, tehát a számításaink helyesek.
Végeredmény:
V1 = 12 V
V2 = 16 V
V3 = 16 V
2
- Még nem érkezett komment!