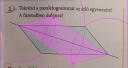
Tengelyes tükrözés

1., 2.
A szerkesztés menete ugyanaz:
    • Bedöföd a körzőt az alakzat egyik tengelyen lévő pontjába
    • Kiszemeled az alakzat egyik nem a tengelyen levő, tehát tükrözendő pontját
    • A körzőt a kiszemelt pontig terpeszted
    • Megrajzolod a kört (ha nem is az egészet, legalább a tengely túloldali részét)
    • Bedöföd a körzőt az alakzat másik tengelyen lévő pontjába
    • A körzőt a kiszemelt pontig terpeszted
    • Megrajzolod a kört (ha nem is az egészet, legalább amennyi metszi az előző kört)
    • Mindkét tengelyen lévő pontot összekötöd a két kör metszéspontjával
A háromszög esetében ennyi, a paralelogramma esetében megismétled a másik tükrözendő pontra is.


2.
A kapott alakzat egy deltoid. A területét kétféleképpen is kiszámoltam, mert nem tudom melyiket várja tőletek a tanár.


`ul"Az eredeti háromszög és a tökörképe területeinek az összege"`

`T_{ABC} = \frac{AB * AC}{2} = \frac{24 * 18}{2} = \frac{432}{2} = 216`

`T_{ABA'C} = \frac{AB * AC}{2} + \frac{A'B * A'C}{2} = \frac{24 * 18}{2} + \frac{24 * 18}{2} = \frac{24 * 18 + 24 * 18}{2} = \frac{\cancel{2} * (24 * 18)}{\cancel{2}} = 24 * 18 = 432`


`ul"Deltoid területe"`

`BC = \sqrt{AB^2 + BC^2} = \sqrt{576 + 324} = \sqrt{900} = 30`

`\hat{ABC} = arctan \frac{AC}{AB} = arctan \frac{18}{24} = arctan \ .75 \approx 36.869898`

`AM = \frac{AB * sin \ \hat{ABM}}{sin \ \hat{AMB}} = \frac{24 * sin \ 36.869898}{sin \ 90} = \frac{24 * .6}{1} = 14.4`

`A A' = AM * 2 = 14.4 * 2 = 28.8`

`T_"deltoid" = \frac{BC * A A'}{2} = \frac{30 * 28.8}{2} = \frac{864}{2} = 432`